Unlocking the Secrets of Alternating Sums from 1996 to 1
Written on
Chapter 1 Understanding Alternating Sums
This alternating sum may appear quite complex due to the squared terms involved. However, anyone with a grasp of fundamental high school algebra should be able to work through it successfully!
What is a²? b²?
I suggest you take a moment to pause, grab a pen and paper, and attempt this problem before reading on for the solution!
Solution
This scenario illustrates the concept of the difference of squares, which we will utilize in our calculations.
We can pair the terms starting with 1996² and 1995², followed by 1994² with 1993², and continue this pattern down to 2² with 1².

Next, let's explore what occurs when we apply the difference of squares formula:
1996² - 1995² = (1996 + 1995)(1996 - 1995) = 1996 + 1995
1994² - 1993² = (1994 + 1993)(1994 - 1993) = 1994 + 1993
…
2² - 1² = (2 + 1)(2 - 1) = 2 + 1
This means our entire expression simplifies to the sum of 1 + 2 + … + 1995 + 1996!
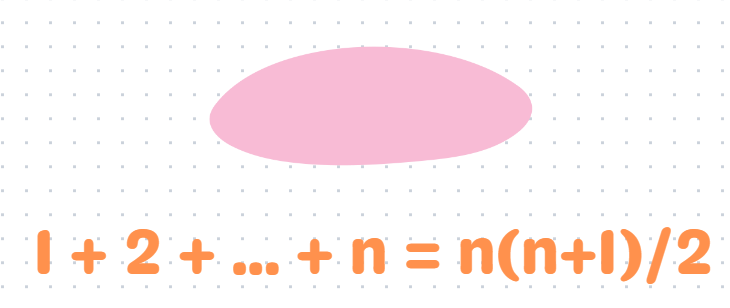
Hopefully, you recall this formula from your school days! Extra credit if you know how to derive it!
To solve our problem, we will set n = 1996.
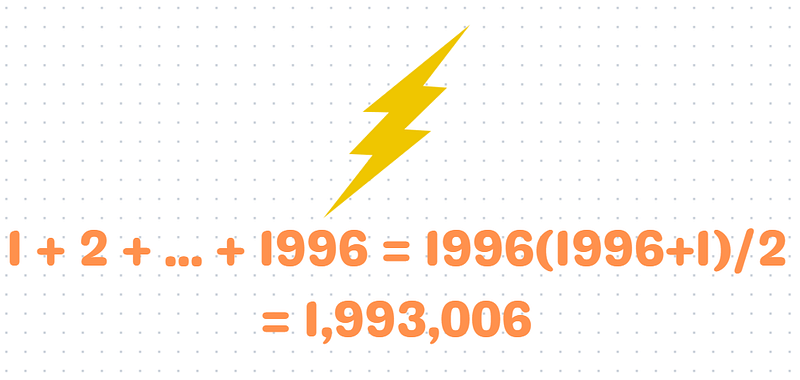
And that leads us to our final answer.

What an incredible journey!
What thought process did you follow this time? I invite you to share your insights in the comments!
Math Puzzles
Explore a collection of the best math puzzles available on Medium, covering topics like Algebra, Geometry, Calculus, and Number Theory.
Bella’s Weekly Math Games
Join a weekly math competition that lasts for 48 hours!
Stay Updated
Sign up to receive notifications whenever I publish new content. Thank you for your support!
Thank you for reading! If you found this article helpful, please consider giving it a clap.

If you feel generous, please buy me a coffee! Your support means the world to me and helps sustain my writing efforts.
Happy Solving,
Bella
If you’d like to connect professionally or just say hello, don’t hesitate to reach out!
Chapter 2 Video Insights
In this section, we'll explore video resources that deepen our understanding of alternating series.
This video titled "Finding the sum of a series with alternating terms" provides a clear explanation of how to approach such sums.
The second video, "Alternating Series Test Example SUM( (-1)^(n + 1)/(n + 7))", offers an illustrative example of applying the alternating series test.