Section 1.1: The Significance of the Golden Ratio

Forget the golden ratio for a moment; let’s turn our attention to the golden integral. In my initial article on Medium, I shared my longstanding admiration for this particular integral.

To fully grasp this topic, I recommend reviewing the previous article, which covers the essential aspects of the golden ratio. We will begin by identifying two critical concepts that will aid us in our calculations.

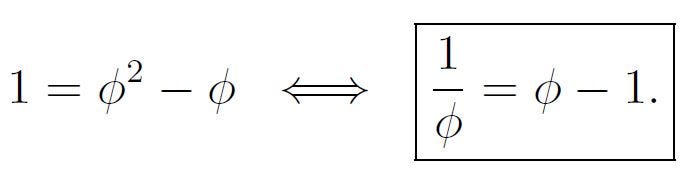
1. The Identity of the Golden Ratio.

Given that ? satisfies the equation x²-x-1=0, we can derive the following relationships:

2. Understanding Gamma and Beta Functions.

If you're unfamiliar with gamma and beta functions, they may seem complex at first. However, I’ll clarify only the aspects necessary for our analysis, ensuring you know what to focus on later.

The gamma function generalizes the factorial function for non-integer values. For any real number x > 0, it is defined as follows:

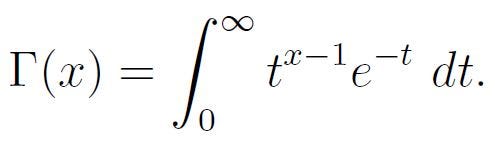
It's essential to remember these two properties of the gamma function:

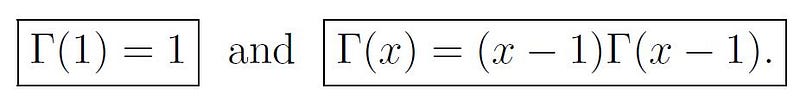
The beta function closely relates to the gamma function, as we will see shortly. In my earlier article, I defined the beta function as follows:

For any real numbers x, y > 0, the beta function is:

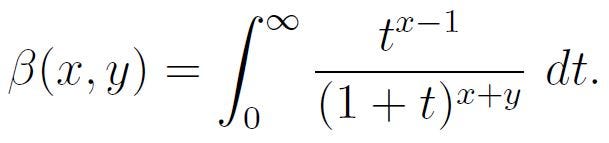
For this discussion, we will utilize an alternative formulation. The beta function can also be expressed using sine and cosine functions:

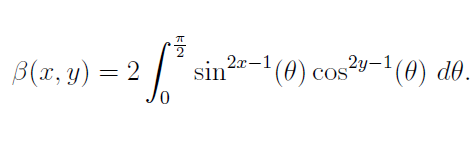
It’s crucial to remember this formulation, as it will be relevant in our calculations. Additionally, the relationship between the beta and gamma functions can be established:

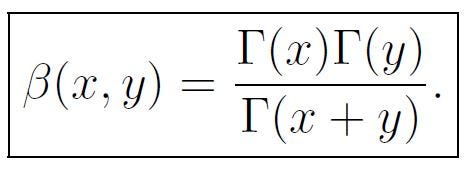
Section 1.2: Solving the Integral

Now that we’ve covered the necessary groundwork, let’s tackle the integral.

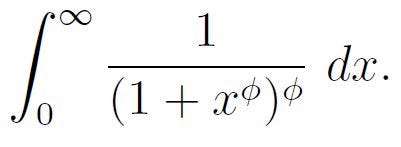
We begin with a substitution. Let:

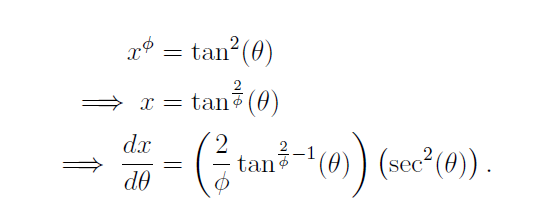
This allows us to reformulate our original integral:

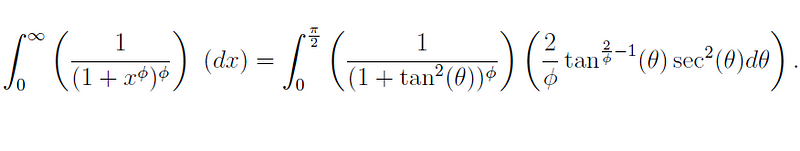
Note that we had to adjust our limits of integration accordingly:

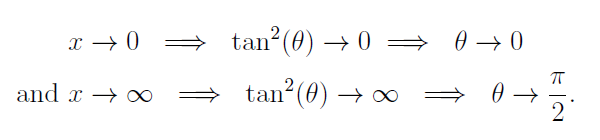
Next, we recall that:

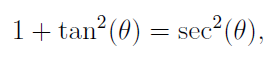
Thus, our integral simplifies to:

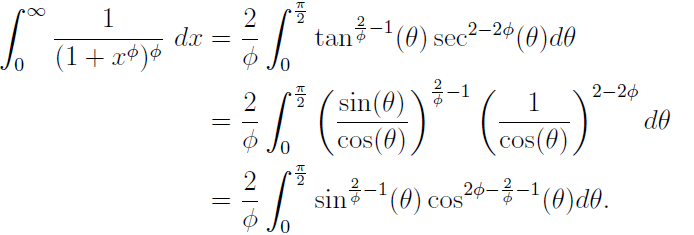
Recognizing that this function aligns with the beta function we defined earlier, we set:

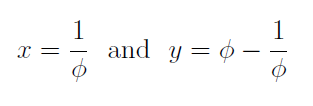
Consequently, we find that:

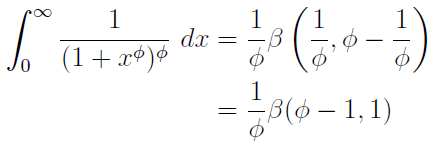
This matches the outcome we reached in the previous article using the first method. Thus, we can conclude our solution similarly.

Utilizing the relationship between the beta and gamma functions, we can compute this integral. Recall that:

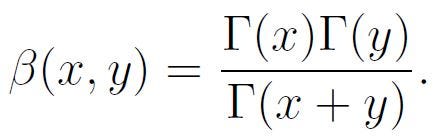
Therefore, we arrive at:

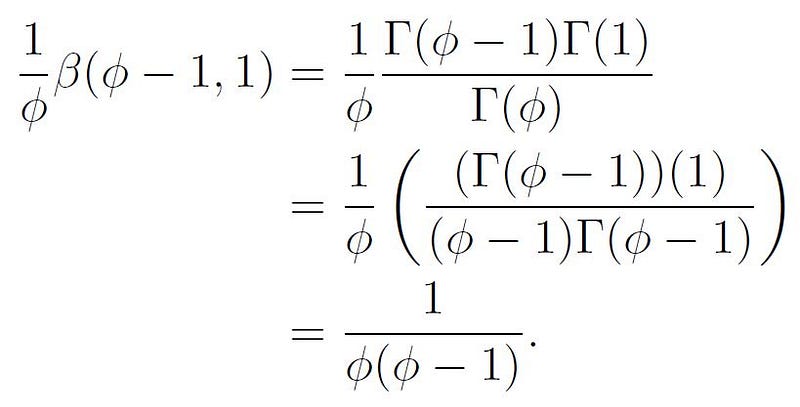
It’s noteworthy that we used the property ?(x)=(x-1)?(x-1) mentioned earlier.

Finally, we must remember that:

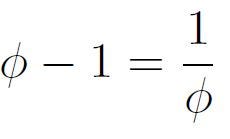
Consequently, we have:

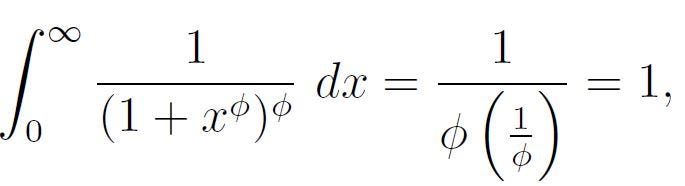
This result is truly remarkable!

I hope you found this alternative approach intriguing and that it added to your understanding of the golden integral. If you enjoyed this article, consider following me and my publication, Y(Math), to help share these insights with a broader audience.

The second video titled "A Golden Ratio Integral" offers additional context and depth to the concepts discussed in this article.