Chapter 1: The Allure of Mathematical Puzzles

The Beal Conjecture presents a captivating enigma that can keep you pondering late into the night.

Photo by Craig Whitehead on Unsplash

This unsolved conundrum is straightforward to grasp but remarkably challenging to resolve. It is so formidable that D. Andrew Beal, a well-known banker and math enthusiast, has pledged a reward of one million dollars for anyone who can provide a correct solution.

In the field of mathematics, numerous problems are deemed so significant that they come with financial rewards. Among the most famous are the seven Millennium Prize Problems, which include renowned challenges like the Riemann Hypothesis and P vs NP. However, there are additional problems with cash bounties, one of which is the Beal Conjecture, the primary focus of this article.

Section 1.1: Understanding Coprime Integers

Two integers, n and m, are regarded as coprime or relatively prime if their greatest common divisor is 1, meaning they share no prime factors. A pair of coprime integers, denoted as (n, m), is referred to as a coprime pair.

All pairs of distinct prime numbers qualify as coprime pairs, as does the pair (9, 4), since no prime number divides both. By definition, a prime number is any positive integer greater than 1, with no divisors other than 1 and itself.

Subsection 1.1.1: The Beal Conjecture Defined

The Beal Conjecture articulates that:

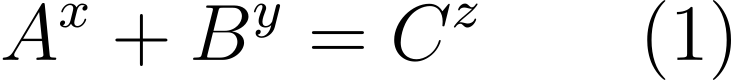
where A, B, C, x, y, and z are natural numbers (positive integers). The conjecture asserts that if x, y, and z exceed 2, then A, B, and C must share a common prime factor.

For instance, consider the equation:

3³ + 6³ = 3?.

In this case, all three terms share the prime factor 3, as 3 divides 3, 6, and 3 respectively. The Beal Conjecture posits that this holds true for all such equations.

To gain a deeper understanding of the phrase "if P then Q," one might explore equivalent forms, such as the contrapositive. Proving the contrapositive of the Beal Conjecture would consequently validate the original statement.

Chapter 2: The Connection to Fermat's Last Theorem

The first video, "The Million Dollar Equation (Navier-Stokes equations) - YouTube," delves into the complexities surrounding the Beal Conjecture.

The second video, "The Million Dollar Equations - with Tom Crawford - YouTube," further explores the implications of this mathematical mystery.

The road to uncovering a million-dollar solution is no easy task. The proof must be published in a peer-reviewed journal recognized by the AMS, and the difficulty of this conjecture is substantial. Indeed, the Beal Conjecture generalizes Fermat’s Last Theorem (FLT), which asserts that there are no natural number solutions for the equation

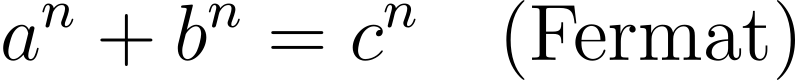
for n ≥ 3. Proving FLT took mathematicians 350 years, and the proof itself is intricate, relying on modern, specialized mathematics that only a select few can fully comprehend.

The Beal Conjecture is, by all accounts, a more complex challenge than FLT. For anyone to prove the Beal Conjecture, they would need to find a novel approach that has eluded the greatest mathematicians for 350 years.

To illustrate that the Beal Conjecture implies Fermat’s Last Theorem, assume that the Beal Conjecture holds true. If a Fermat-type equation exists with natural numbers a, b, c and an exponent n ≥ 3, then the Beal Conjecture indicates that a, b, and c must have a common factor. By dividing through by that factor, one could derive yet another solution to FLT.

Continuing this process would eventually yield a solution where a and b are coprime, which contradicts the assumption of the Beal Conjecture. Hence, no such solution can exist for n ≥ 3, confirming Fermat’s Last Theorem.

The Beal Conjecture remains a captivating enigma in the realm of numbers. Like Fermat’s Last Theorem, its simplicity can be deceiving, masking the complexity that lies beneath.