Chapter 1: The Intriguing Concept of an Infinite Hotel

What makes a math hotel with endless rooms so captivating? Primarily, it exists solely within the realm of mathematics. Currently, we can only envision infinite rooms in this abstract world. This concept allows us to engage with infinity in a playful manner. Infinity is often an elusive idea, but this thought experiment provides a way for anyone to comprehend and even interact with it.

Imagine this: you are the manager of a fully booked math hotel. A new guest arrives at your door. How will you manage to fit them in?

Accommodating One New Guest

How can you possibly welcome a new guest when the hotel is at full capacity? Instinct might tell you it's impossible, and you may consider turning them away. However, remember, this is an infinite math hotel! Infinity is not merely a number; it’s a concept. The number of rooms transcends what we can count as humans. To make space, simply ask each current guest to shift one room to the right (incrementing their room number by one). This action leaves the first room vacant, allowing the new guest to settle in.

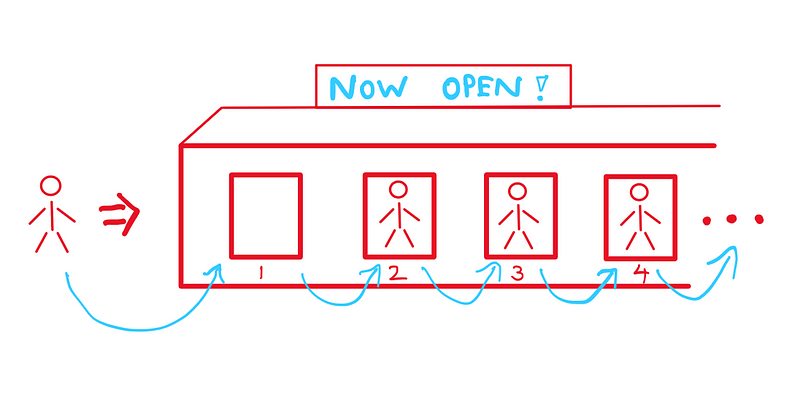
Accommodating Multiple Guests

If several guests arrive, instruct each existing guest to move to a room number that equals their current number plus the total number of new arrivals. For instance, if 13 new guests show up, the guest in room 40 would move to room 53 (40+13). If this still seems perplexing, remember that this paradox arises from the intriguing nature of infinity.

How the Infinite Hotel Operates

This fascinating thought experiment was devised by the notable German mathematician David Hilbert, who played a significant role in the development of modern mathematics during the 19th and 20th centuries. His students, including Jon Von Neumann and Richard Courant, also made substantial contributions to the field. Hilbert's hotel serves to illustrate the complexities associated with the concept of infinity. Since infinity isn't a finite number and has no upper limit, guests can always be accommodated by repositioning existing guests.

Can the Hotel Host Infinite Guests?

What if a spaceship arrives, carrying an infinite number of guests? Could you still provide them with rooms? The answer is yes! To manage this influx, ask every current guest to double their room number. This will leave all odd-numbered rooms available.

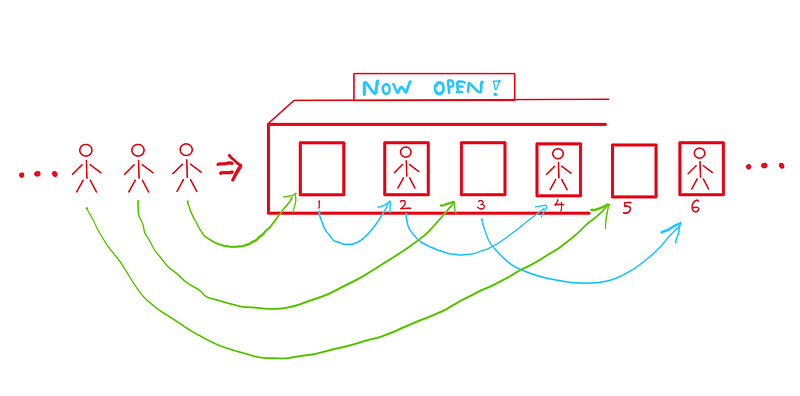
Since guests now occupy rooms that are multiples of 2, all odd-numbered rooms—extending to infinity—remain open. Thus, you can welcome an infinite number of new guests to your math hotel. It’s a mind-bending notion, isn’t it? But the game doesn't end there!

Infinite Spaceships Arriving at Once

Now, imagine multiple spaceships, each filled with infinite guests. How will you manage this? You can still accommodate them! First, instruct all current guests to move to their room number multiplied by 2, keeping all odd-numbered rooms free as before.

For passengers in spaceship one, assign them room numbers of 3^n, where n represents their seat number. For instance, the first passenger takes room 3, the second takes room 9 (3²), and so forth. Passengers from spaceship two would take room numbers of 5^n, and so on for subsequent spaceships, using the next prime number.

Where Does the Game End?

How far can we extend this layering of infinity? While we can continue to build upon these layers, the process must stop at a finite number of infinite layers. Not all infinities are equal, and a deeper exploration of this will be addressed in a future discussion. For now, you’ve had a glimpse into the intriguing nature of infinity, which cannot be treated like a typical countable number.

Ultimately, every human who has ever lived could find a room in your infinite math hotel!

I hope you found this exploration engaging and enlightening. If you wish to support my work, feel free to clap, follow, or subscribe for more content.

For further reading, you might enjoy articles like "What Really Happens When You Invent Infinite Infinities?" and "Why Do We Really Use The 12-Hour Clock?"

You can read the original essay here.