Exploring Triangular Differential Equations: A Deep Dive
Written on
Chapter 1: Understanding the Triangular Differential Equation
When dealing with a triangular differential equation, we can be assured that there exists a solution. However, visualizing a function whose derivative equals the square of its cosine can be quite challenging. The strategy employed here is called separation of variables, which entails rearranging the equation so that all terms involving y are on one side and all terms involving x are on the other.
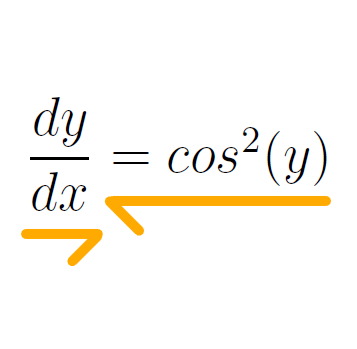
The secant function, represented as sec, is the reciprocal of cosine. It's crucial to remember that the integral of sec² results in tan, a fact that can be verified through differentiation. Thus, we can now proceed to integrate both sides of our equation concerning x.
Section 1.1: Integration Process
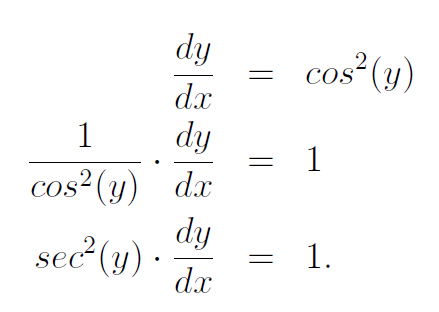
In our integration, C represents a constant of integration, as we are working with indefinite integrals. Additionally, we've performed a variable change to integrate the left side with respect to y, effectively eliminating the dx term. This simplification allows us to easily derive our solution—simply apply the inverse tangent.
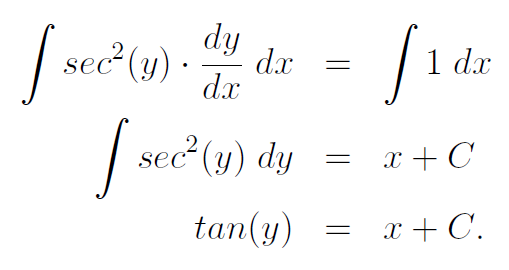
Now we arrive at the general solution for our differential equation. To refine our solution, we can set C to 0 under specific initial conditions. For instance, if y equals 0 when x is 0, then C becomes 0, leading us to:
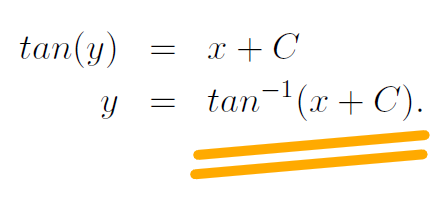
Section 1.2: Verifying the Solution
You might still question whether this solution fulfills the original differential equation, as I initially did. Thus, let's verify it. The derivative of the inverse tangent is crucial for this process.
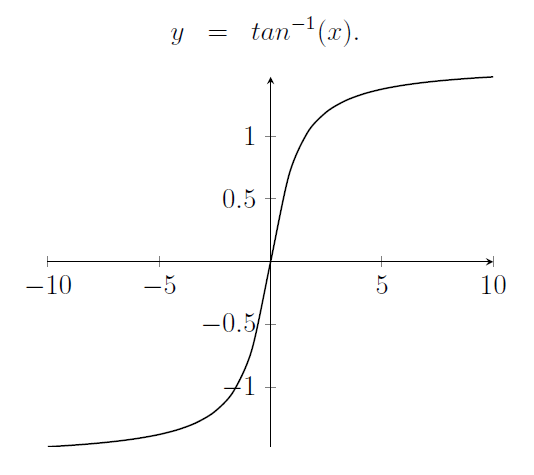
By recalling the original differential equation, we can confirm that:
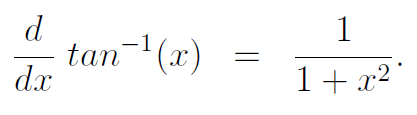
This holds true. A straightforward way to grasp it is to visualize a right triangle with side lengths and angles that correspond to our equation. Let's consider an arbitrary angle θ in such a triangle and build our understanding from there.
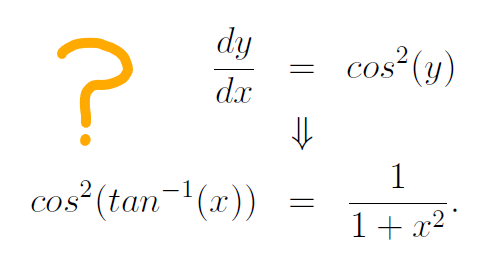
To find the cosine of θ, we need to square it. Assuming θ is the inverse tangent of x, we can express this as:
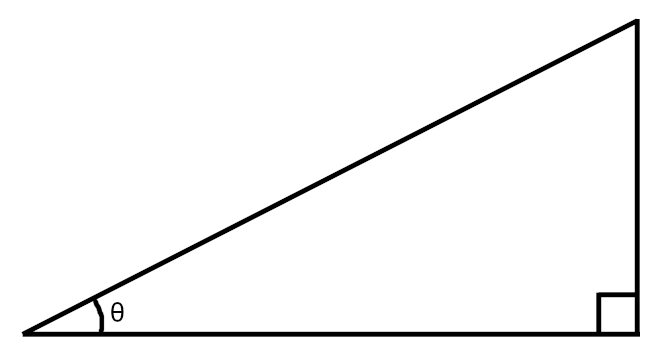
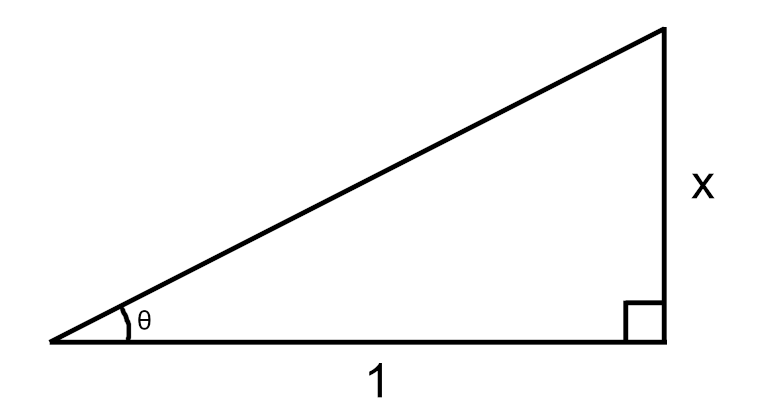
In a right triangle, the tangent of an angle is defined as the ratio of the length of the opposite side to the length of the adjacent side. We'll select side lengths such that the ratio opposite/adjacent equals x.
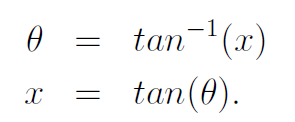
To calculate the cosine of θ, we find the ratio of the adjacent side to the hypotenuse. The hypotenuse can be determined using the Pythagorean Theorem.
Next, we take the cosine of θ and then square it.
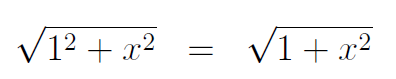
Remember that θ is the inverse tangent of x; hence, we make one final substitution:
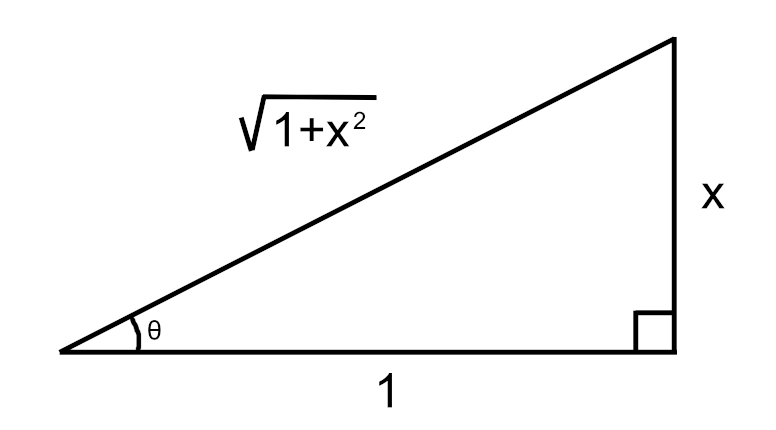
This confirms our solution to the differential equation. Although this discussion has focused more on triangles than on differential equations, it's rewarding to see such a neat resolution to a non-linear differential equation.
Chapter 2: Visualizing the Solution
To further illustrate these concepts, the following video resources provide valuable insights.
The first video, "Constructing Triangle Method (CTM) to Solve Trigonometric Differential Equation," explains various techniques used in solving these equations.
The second video, "A Pythagorean differential equation," delves into the relationship between differential equations and the Pythagorean theorem.