Geometry Puzzle: Can You Calculate the Shaded Area?
Written on
Chapter 1: The Geometry Challenge
Recently, I encountered an intriguing geometry problem. The illustration features four adjacent circles, each touching the sides of an equilateral triangle with side lengths of 3. The challenge is to determine the area of the shaded section.
As a tip: mathematics often rewards those who leverage its inherent symmetry, so let's take advantage of that principle! I suggest you pause here, grab a pen and paper, and attempt to solve it before continuing for the solution.
Solution
The symmetry of the figure suggests that the three smaller circles share the same radius. Our goal is to identify the radii of both the larger and smaller circles.
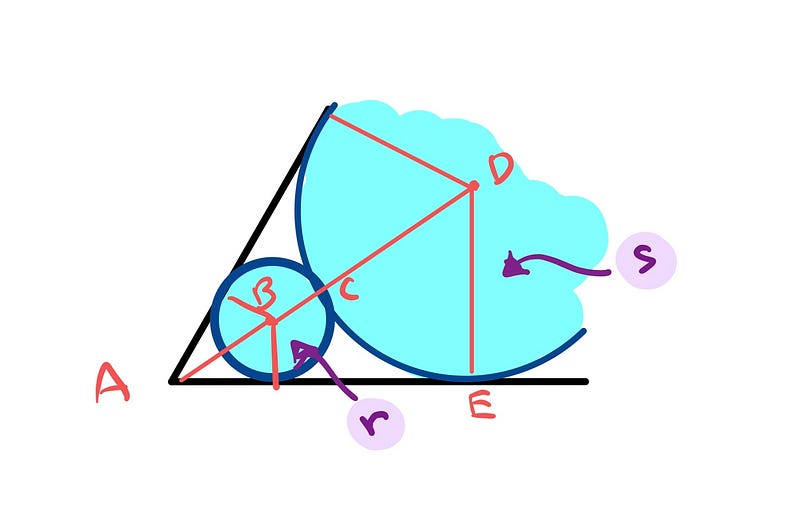
In the diagram, points A, B, C, D, and E are marked. Let the radius of the larger circle be denoted as ( s ) and the radius of the smaller circle as ( r ).
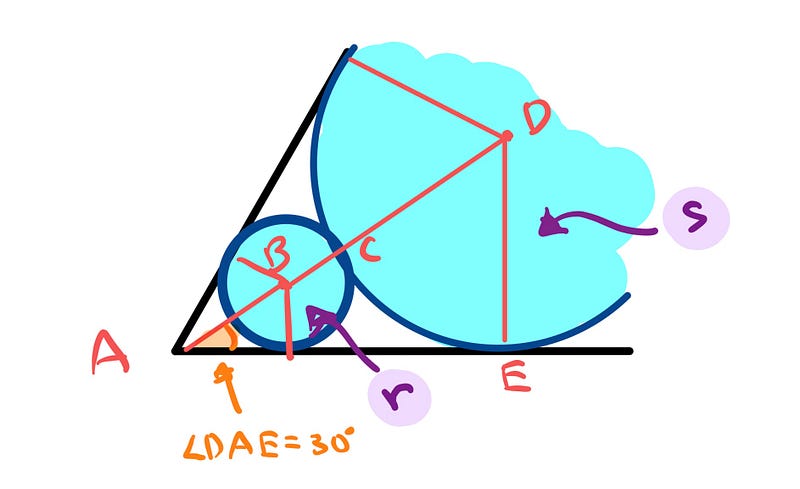
Examining the diagram closely, angle DAE measures 30 degrees because each angle in an equilateral triangle is 60 degrees.
Do you see how to proceed from here? We will look at triangles with hypotenuses AB and AD, respectively.
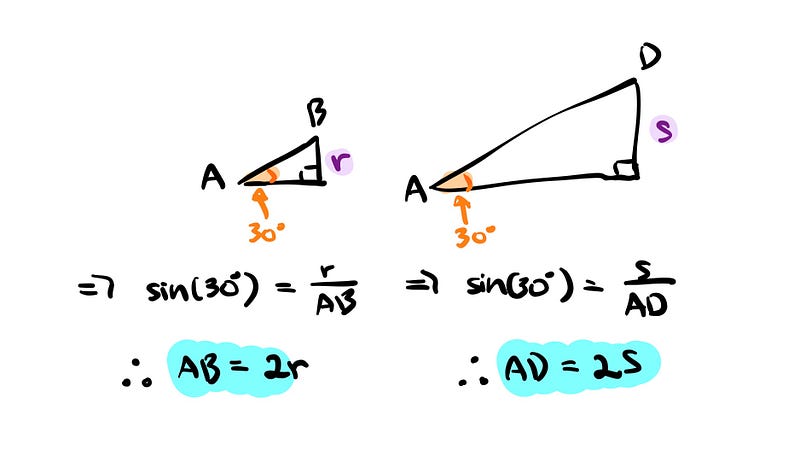
Using the SOH-CAH-TOA trigonometric ratios, we can express the lengths of AB and AD in terms of ( r ) and ( s ):
- ( AB = 2r )
- ( AD = 2s )
Now, revisiting the diagram:
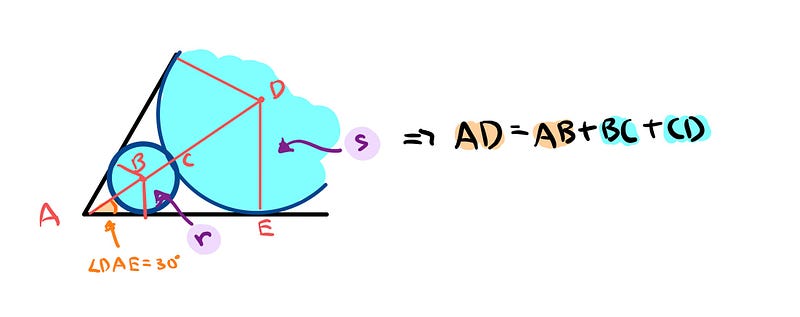
We find that ( AD ) equals the sum of ( AB ), ( BC ), and ( CD ). Knowing ( AD ) and ( AB ) in terms of ( r ) and ( s ), we now need to determine ( BC ) and ( CD ). Here, ( BC ) is simply the radius of the smaller circle, which is ( s ), while ( CD ) is the radius of the larger circle, denoted ( r ).
Thus, we have the following equation:
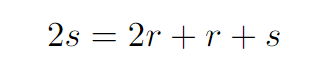
From this, we derive:
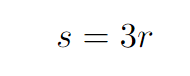
Next, we consider triangle ADE, where the length of AE is half of 3.
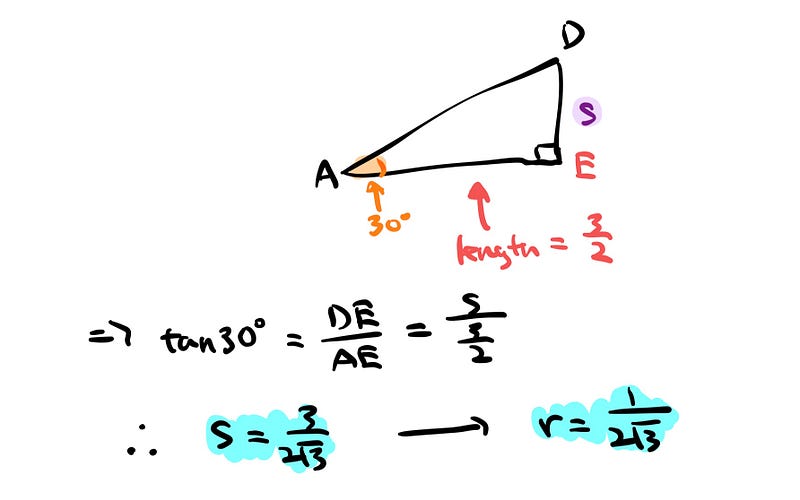
Applying the SOH-CAH-TOA ratios once more, we can calculate the values of ( s ) and ( r ). The total area of the shaded section is the sum of the area of one large circle and three smaller circles.
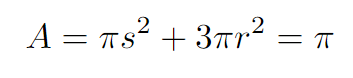
Isn’t it fascinating? Here’s a cute dog as a reward for your efforts! 🐶

Congratulations on reaching the solution! What was your thought process this time? Please share your insights in the comments below; I'm eager to hear from you!
Math Puzzles
Explore more captivating math puzzles in various domains including Algebra, Geometry, Calculus, and Number Theory!
The first video, "Area of Shaded Region - Circles, Rectangles, Triangles, & Squares - Geometry," delves into calculating the areas of different shapes and their shaded regions.
The second video, "How to Find the Area of the Shaded Region | Rectangle in a Rectangle | Math with Mr. J," offers additional insights into finding areas within complex shapes.
Thank you for reading! If you found this article helpful, please consider giving it a clap!

If you appreciate my work, feel free to buy me a coffee! Your support means a lot and helps me continue creating engaging content.
With gratitude, Bella ❤️