A Deep Dive into the 2024 Japanese Preliminary Olympiad Problem
Written on
Chapter 1: Introduction to the Problem
Can you tackle this challenge from the 2024 Japanese Preliminary Olympiad? Here we present a problem from that event. In this context, the notation on the left represents the floor function, which indicates the greatest integer less than or equal to the given number. For instance, ⌊5.6⌋ = 5. Meanwhile, on the right side, we encounter a binomial coefficient. We will begin our exploration, but as is customary, readers are encouraged to attempt the problem themselves before reviewing the solution!
To facilitate our understanding, let's introduce a new notation: the product symbol. We will denote this as follows:
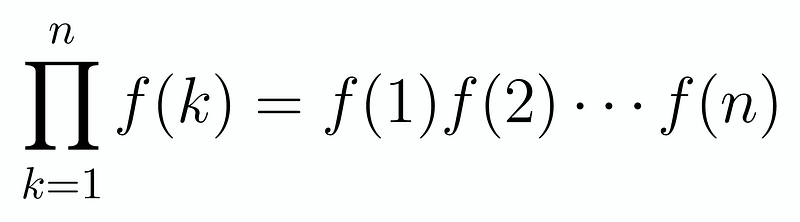
In simpler terms, f(k) takes every value of k from 1 to n and multiplies them together. With this in mind, let’s express our problem using product notation. First, pay attention to the following:
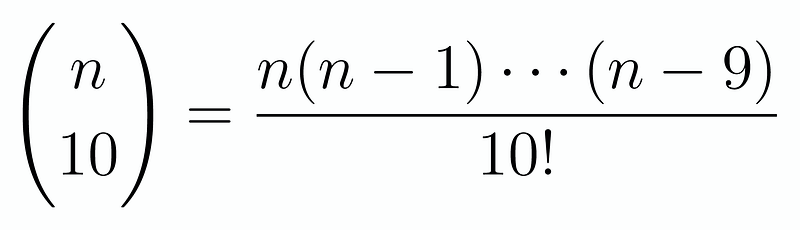
Now, we can reformulate our original equation in terms of products:
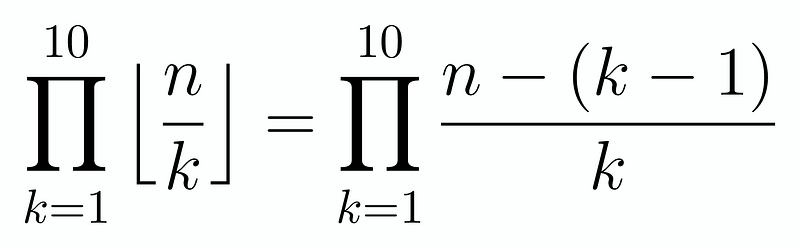
Take note of the following inequality:
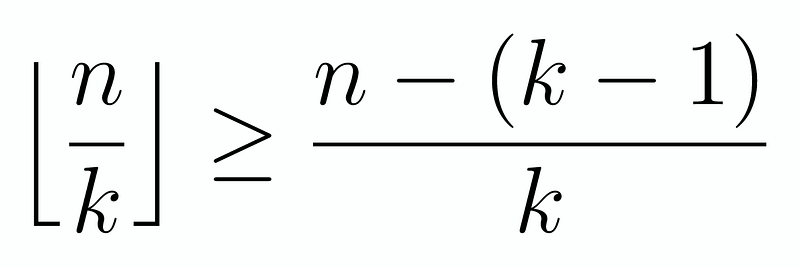
While it may not be immediately apparent, if we expand this expression, it indeed holds true. This is because multiplying the floor function by k can lead to various outcomes. If we have an exact division, the result is evidently larger. Conversely, if the division isn't exact, the k-1 factor ensures we revert to our multiple, thereby making it greater than or equal. The critical question is: under what conditions do we achieve equality? Let’s rewrite this as follows:
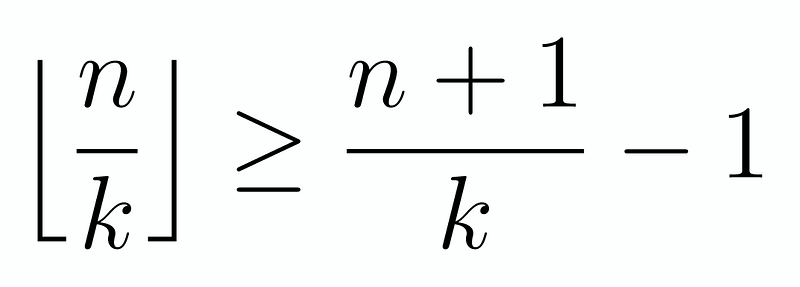
From this, it becomes evident that for equality to be true, (n+1)/k must be an integer. This condition also guarantees that n/k is NOT an integer, as (n+1)/k is precisely one unit more than ⌊n/k⌋. In simpler terms, equality holds when k divides n+1. From our product inequality, it is clear that this condition must apply to each k. Thus, the solution is the smallest n such that all integers from 1 to 10 can divide n+1.
Identifying this number is straightforward (we can simply analyze prime factors), and we discover that the smallest n+1 is 2520. Consequently, our final result is n = 2519.