Importing the SymPy Library

To kickstart our Python project, we need to import the necessary libraries. In this case, we'll utilize the SymPy library, which provides all the tools we need for differentiation and integration, along with several other handy functions.

# Importing the library

import sympy

Defining Symbols

With SymPy ready to go, we can define our symbols, which will be integral to formulating our equations. The Symbol class allows us to create these symbols, and it’s a good practice to use a string that corresponds with the variable name.

# Defining symbols

x = sympy.Symbol("x")

y = sympy.Symbol("y")

Creating an Equation

Let’s formulate an equation using the symbols we've defined. Here’s how we can create a simple expression:

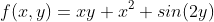
The corresponding code for this equation is as follows:

# Creating the equation

f = x * y + x ** 2 + sympy.sin(2 * y)

Differentiation

To find the derivative of our equation, we can utilize the diff function from the SymPy library. Given that our equation has two variables, we can differentiate it with respect to either. In this instance, let’s differentiate with respect to x.

# Differentiate with respect to x

df_dx = sympy.diff(f, x)

print("The derivative of f(x,y) with respect to x is: " + str(df_dx))

Output:

The derivative of f(x,y) with respect to x is: 2*x + y

This result aligns with our expectations. The diff function also supports higher-order derivatives. For example, we can calculate the second derivative with respect to y as follows:

# Second derivative with respect to y

d2f_dy2 = sympy.diff(f, y, 2)

print("The second derivative of f(x,y) with respect to y is: " + str(d2f_dy2))

Output:

The second derivative of f(x,y) with respect to y is: -4*sin(2*y)

Integration

SymPy makes symbolic integration straightforward as well. Using the same equation, we can integrate with respect to x:

# Integrate with respect to x

F = sympy.integrate(f, x)

print("The integral of f(x,y) with respect to x is: " + str(F))

Output:

The integral of f(x,y) with respect to x is: x**3/3 + x**2*y/2 + x*sin(2*y)

Additionally, we can perform definite integration. Here’s how to integrate our original equation with bounds from 0 to 2:

# Definite integral with respect to x [0, 2]

F = sympy.integrate(f, (x, 0, 2))

print("The definite integral of f(x,y) with respect to x with bounds [0, 2] is: " + str(F))

Output:

The definite integral of f(x,y) with respect to x with bounds [0, 2] is: 2*y + 2*sin(2*y) + 8/3

Other Useful Functions in SymPy

While this article primarily covers differentiation and integration, SymPy offers several other valuable functions. These can assist in making your outputs clearer and more manageable. Two functions that I frequently use are:

• Simplify: This function helps in reducing an equation to a more straightforward form. For instance:

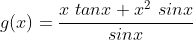
# Simplifying equations

g = (x * sympy.tan(x) + x ** 2 * sympy.sin(x))/sympy.sin(x)

g = sympy.simplify(g)

print("The simplified form of g(x) is: " + str(g))

Output:

The simplified form of g(x) is: x*(x + 1/cos(x))

• Solve: This function is perfect for solving systems of algebraic equations. To use it, we must format the system so that one side equals zero. Here’s an example with a set of equations:

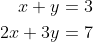
# Solving the system of equations

sol = sympy.solve((x + y - 3, 2 * x + 3 * y - 7), (x, y))

print("The solution of the system is (x, y): (" + str(sol[x]) + ", " + str(sol[y]) + ")")

Output:

The solution of the system is (x, y): (2, 1)

Now you're equipped to perform differentiation and integration using Python! These functions can serve as a helpful double-check for your work or provide quick solutions (just remember to verify the math!).

Thank you for reading! If you have any questions, feel free to leave a comment. If you enjoyed this article, consider following me and exploring my other writings on Python and engineering topics!