Mastering Projectile Motion: A Comprehensive Guide to Ballistics
Written on
Chapter 1: Understanding Ballistics
Ballistics is a field within mechanics focused on the movement of projectiles that are launched into the atmosphere or beyond. This area of study is crucial for understanding how objects behave when propelled.

Physics encompasses the study of matter and waves in the universe. Within physics, mechanics investigates forces, matter, energy, work, and motion. Kinematics, a subset of mechanics, specifically examines motion, while ballistics focuses on projectiles in various environments, including air, water, and space. To address ballistic challenges, we apply the kinematic equations of motion, commonly referred to as the SUVAT equations or Newton’s equations of motion.
For simplicity, we will exclude the effects of air resistance, commonly known as drag, in the following examples. For a deeper understanding of fundamental concepts, refer to my article on Force, Weight, Newtons, Velocity, Mass, and Friction.
Section 1.1: The Equations of Motion (SUVAT Equations)
When considering an object with mass m acted upon by a force F over a time t, it experiences an acceleration represented by a. The object begins with an initial velocity u, and after time t, it reaches a final velocity v while covering a distance s. Thus, we identify five essential parameters related to the motion of the object: s, u, v, a, and t.
The equations of motion enable us to determine any of these parameters, provided we know three others. The three most significant equations are:
- v = u + at
- s = ut + ½at²
- v² = u² + 2as
According to Newton's second law, F = ma, indicating that the acceleration of an object depends on the applied force F and its mass m. An object accelerates and increases speed while a force is applied, but will decelerate if the force opposes its motion. Once the force is removed, the object's velocity remains constant unless acted upon by another force (as stated by Newton’s first law). In our examples, gravity serves as that other force, influencing the velocity to either increase or decrease. While drag typically reduces velocity, we will ignore it for simplicity.
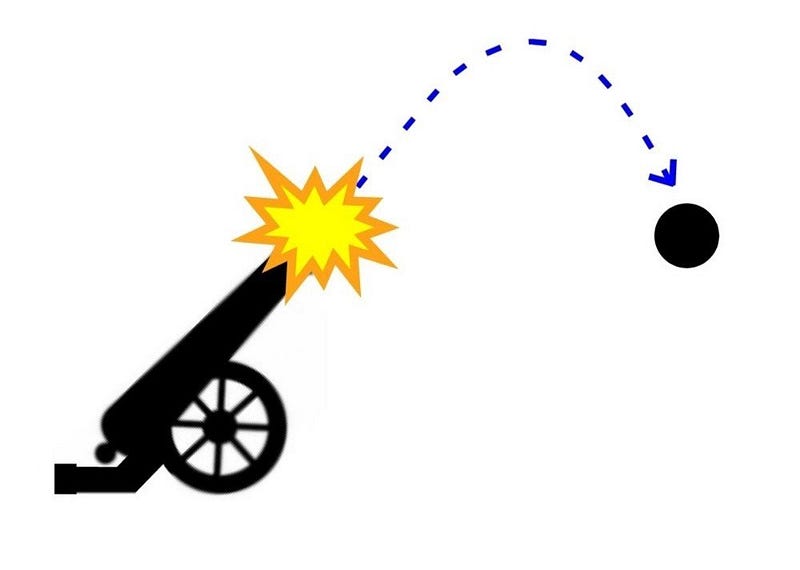
Section 1.2: Analyzing Projectile Motion
To solve projectile motion problems, students often need to calculate time of flight, distance traveled, and maximum altitude. Typically, these questions can be categorized into four scenarios:
- An object dropped from a known height.
- An object thrown upwards.
- An object thrown horizontally from an elevated position.
- An object launched at an angle from the ground.
By examining the initial and final conditions, we can derive formulas for various parameters, including velocity, distance, time of flight, and altitude. Selecting the appropriate equation depends on which parameters are known, allowing us to solve for the unknown parameter.
In examples three and four, we can break down the motion into horizontal and vertical components to find the necessary solutions.
Chapter 2: The Parabolic Path of Projectiles
Unlike guided missiles, which follow a controlled trajectory through advanced technology, a projectile—such as a football, stone, or shell—follows a parabolic path once launched. The initial force imparted by the launching mechanism (e.g., a gun or a hand) gives the body its initial velocity. The subsequent trajectory is a direct result of this initial acceleration.
For more insights on parabolas, check out my tutorial titled "How to Understand the Equation of a Parabola, Directrix, and Focus."

Example 1: Free Fall from a Known Height
Using the equations:
- v = u + at
- s = ut + ½at²
- v² = u² + 2as
In this situation, the object starts from rest, reaching a final velocity v. The acceleration is a = g, where g is the acceleration due to gravity. It is important to note the sign of g, which we will elaborate on later.
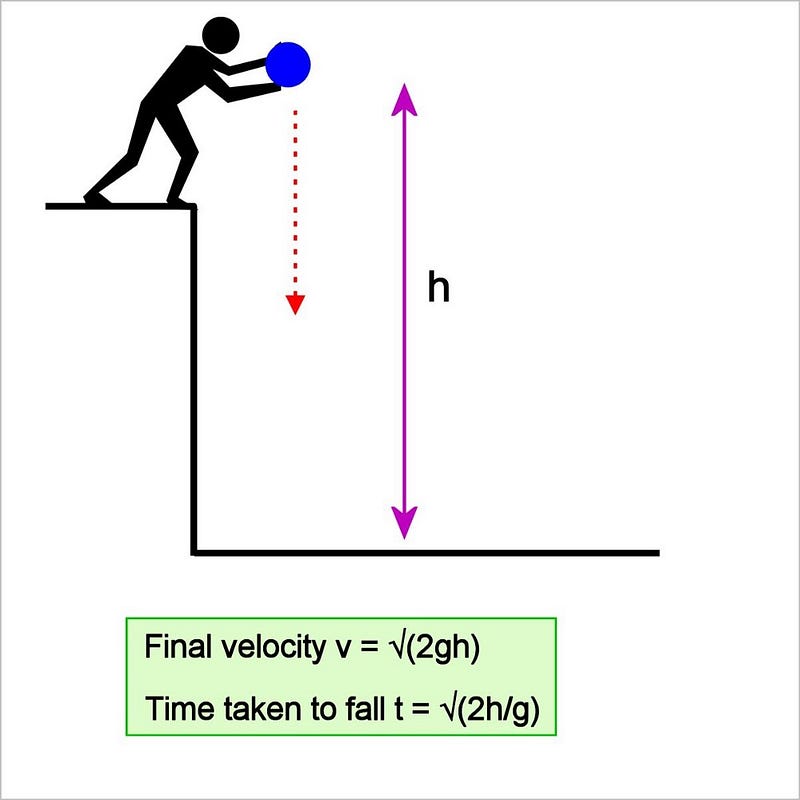
Calculating Final Velocity with Unknown Time
Since the object is initially at rest (u = 0) and we know the height (s = h), we cannot use v = u + at because time (t) is unknown. Instead, we apply:
v² = u² + 2as
= 0² + 2gh
Thus:
v = √(2gh)
Determining Distance Fallen with Unknown Height
Using:
s = ut + ½at²
= 0t + ½gt²
We find:
s = ½gt²
Calculating Time to Fall Distance h
Setting s = h gives us:
h = ½gt²
Thus:
t² = 2h/g
Taking the square root results in:
t = √(2h/g)
Example 2: Object Projected Vertically Upwards
In this scenario, an object is projected straight up at 90 degrees to the ground with an initial velocity u. The final velocity v reaches zero at the maximum height before descending. Here, the acceleration is a = -g, as gravity decelerates the object during its ascent.
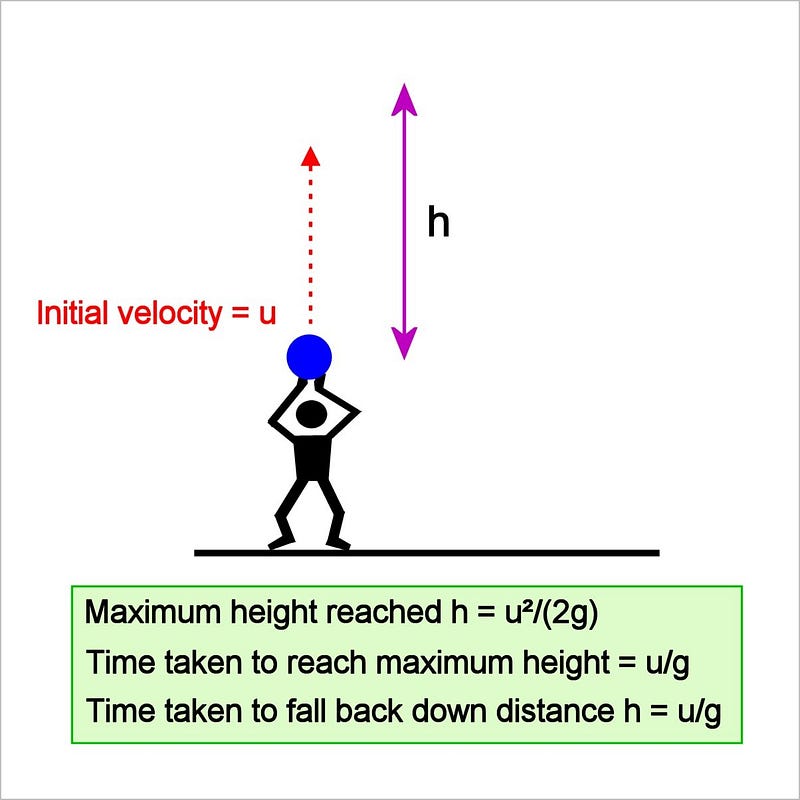
Calculating Time of Flight Upwards
Using:
0 = u + (-g)t
This results in:
u = gt,
which leads to:
t_up = u/g
Calculating Distance Traveled Upwards
Using:
0² = u² + 2(-g)s
This simplifies to:
s = h = u²/(2g)
Calculating Time of Flight Downwards
The time to fall a distance h, as determined in Example 1, is:
t = √(2h/g).
Substituting h yields:
t_down = u/g.
Thus, the total time of flight equals:
t_total = 2u/g.
Example 3: Object Projected Horizontally from Height
For a body projected horizontally from height h with an initial velocity of u, the vertical motion mirrors that of an object dropped from height h. While the object moves forward, it also descends due to gravitational acceleration.
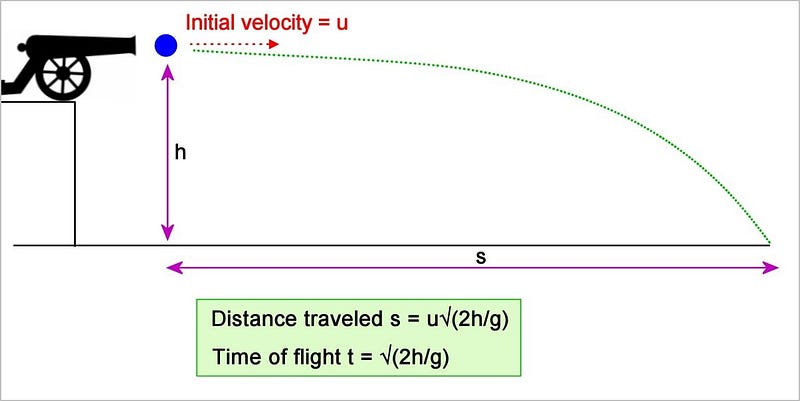
Time of Flight
t = √(2h/g) as derived in Example 1.
Distance Traveled Horizontally
Since there’s no horizontal acceleration, the horizontal distance is calculated as:
Distance = velocity x time = ut = u√(2h/g).
Example 4: Object Projected at an Angle
In this scenario, a projectile is launched at an angle θ with an initial velocity u. This problem is more complex, but we can resolve the velocity vector into horizontal and vertical components.
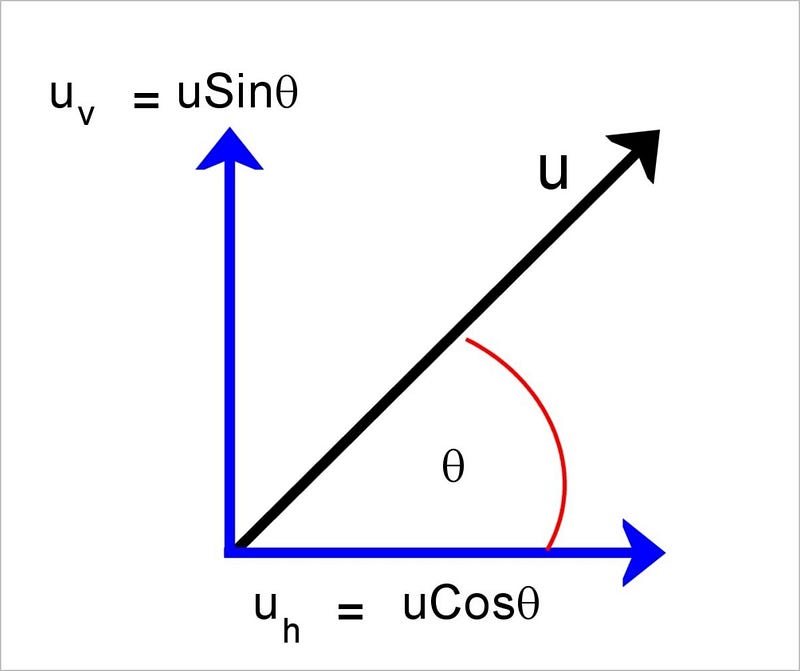
Let u_x be the horizontal component and u_y the vertical component of the initial velocity:
- cos θ = u_x / u → u_x = u cos θ
- sin θ = u_y / u → u_y = u sin θ
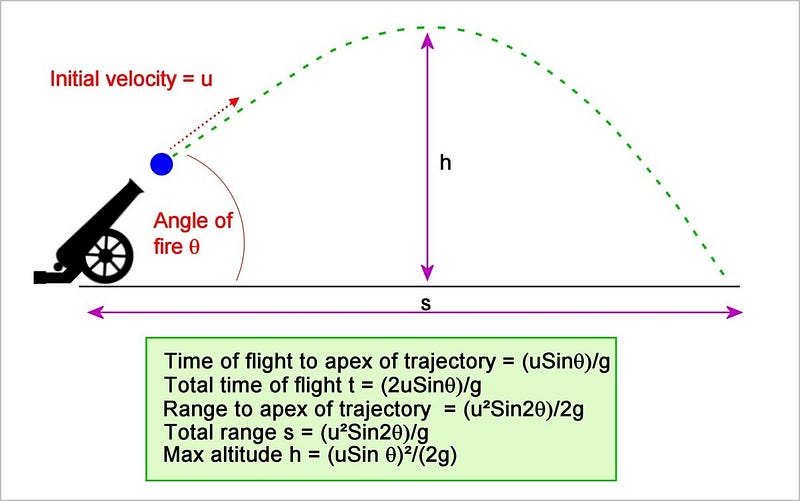
Time of Flight to Apex
From Example 2, the time of flight is:
t = u_y/g = u sin θ/g.
Altitude Attained
Using:
s = u_y²/(2g) = (u sin θ)²/(2g).
Horizontal Distance Traveled
The total time of flight is:
2u sin θ/g.
During this time, the object moves horizontally at velocity u_x = u cos θ, so the horizontal distance is:
Horizontal distance = u cos θ x (2u sin θ)/g,
resulting in:
(2u² sin θ cos θ)/g.
Utilizing the double angle formula, we simplify to:
(u² sin 2θ)/g.
Thus, the horizontal distance to the apex is:
(u² sin 2θ)/2g.
Recommended Reading Materials
Mathematics:
"Engineering Mathematics" by KA Stroud is an essential reference that covers a broad range of mathematical topics, suitable for engineering students and those interested in mathematics.
Mechanics:
"Applied Mechanics" by John Hannah and MJ Hillier is a standard textbook for engineering diploma and technician courses, encompassing foundational concepts relevant to this discussion.
What is the Optimal Launch Angle for a Projectile?
The optimal angle for launching a projectile to achieve maximum horizontal distance is 45 degrees.
Using differential calculus, we can analyze the horizontal range function relative to the angle θ, deriving the angle that maximizes the range.
The horizontal range is expressed as:
R = (u² sin 2θ)/g.
Setting the derivative of this function to zero allows us to find the angle that maximizes the range.
Orbital Velocity Formula: Understanding Satellites and Spacecraft
When an object is projected with sufficient velocity, it can enter an orbit. The orbital velocity is approximately 25,000 km/h at low Earth orbit.
For small objects relative to the larger body being orbited, the velocity can be approximated as:
v ≈ √(GM/r),
where M is the mass of the larger body, r is the distance from the center, and G is the gravitational constant.
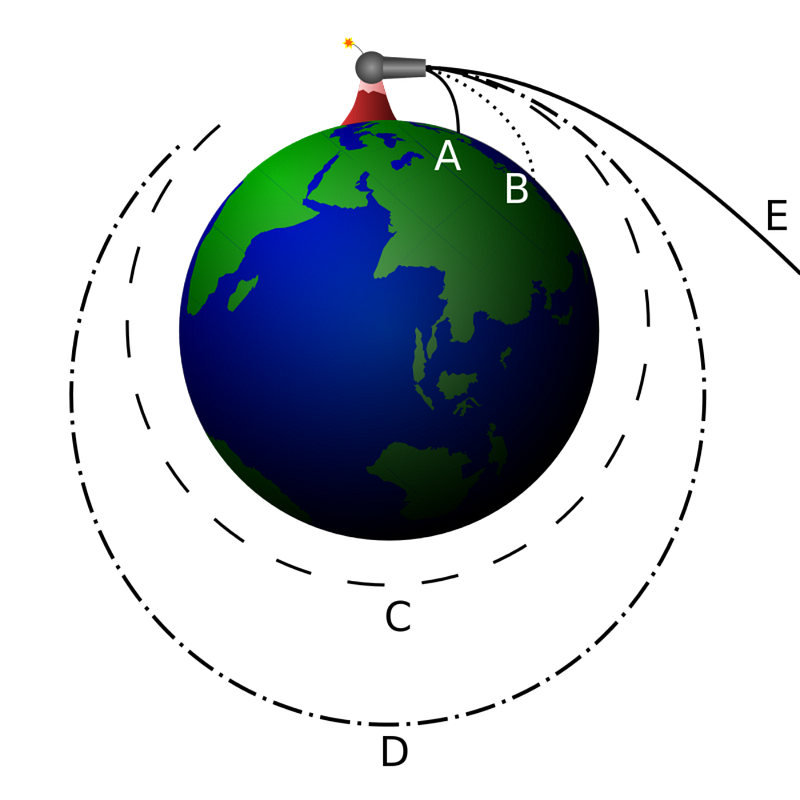
If an object exceeds the required orbital velocity, it will escape the gravitational influence of the planet. This principle was utilized during the Apollo 11 mission, where precise timing and velocity control were critical for lunar insertion.

A Brief Historical Overview
ENIAC (Electronic Numerical Integrator And Computer) was one of the first general-purpose computers, developed during World War II and completed in 1946. It was initially funded by the U.S. Army to compute ballistic tables, factoring in drag, wind, and other influences on projectile motion.
ENIAC was a massive machine, weighing 30 tons and consuming 150 kilowatts of power, occupying 1800 square feet. It was referred to as “a human brain” at the time and utilized vacuum tubes for electronic functions, each requiring significant power and maintenance.


References
Stroud, K.A., (1970) Engineering Mathematics (3rd ed., 1987) Macmillan Education Ltd., London, England.
Hannah, J. and Hillier, M. J., (1971) Applied Mechanics (First metric ed. 1971) Pitman Books Ltd., London, England.
This article was first published on Hubpages on May 20, 2014.