Mastering Rotation Matrices with SymPy: A Comprehensive Guide
Written on
Chapter 1: Introduction to Computer Algebra Systems
Understanding how to navigate computer algebra systems can be quite challenging, but with consistent practice, mastery is attainable. This series is designed to guide you through various mathematical problems using tools like SymPy, Sage, and Mathematica.
Daily Exploration of Computer Algebra
This series tackles both common and unique challenges utilizing SymPy, Mathematica, Sage, and more.
Today’s Focus: Rotation Matrix Calculation
We aim to determine the rotation matrix R that transforms the vector
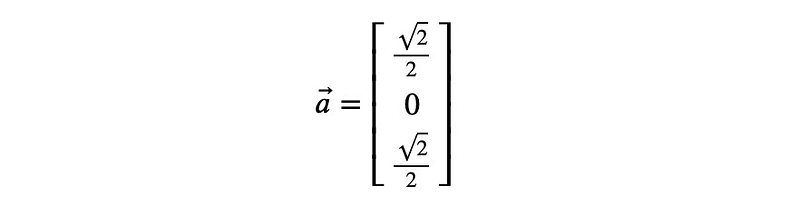
into the vector
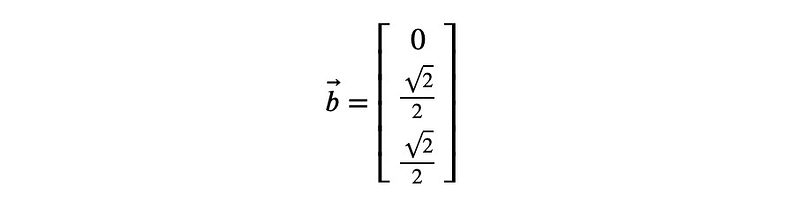
Solution via SymPy
Our task is to identify a 3x3 matrix
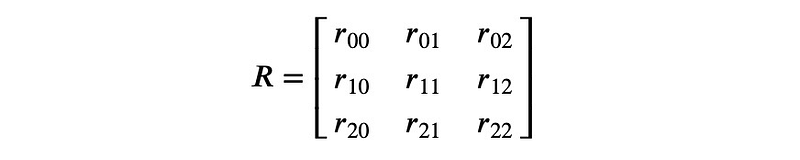
This matrix comprises nine unknowns, necessitating nine equations to solve for them. The goal is for R to convert the vector A into B:
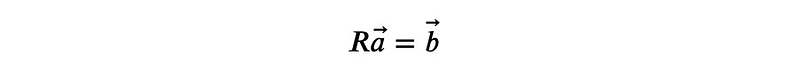
In SymPy, we start by defining both the column vectors and the matrix containing the unknowns:
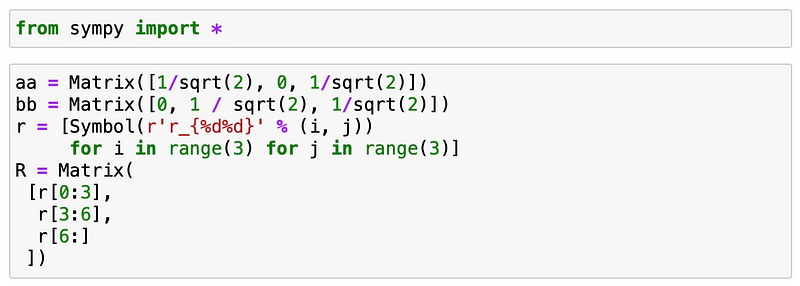

The initial equation we have is:

This equation can be interpreted as three distinct equations, one for each vector component:
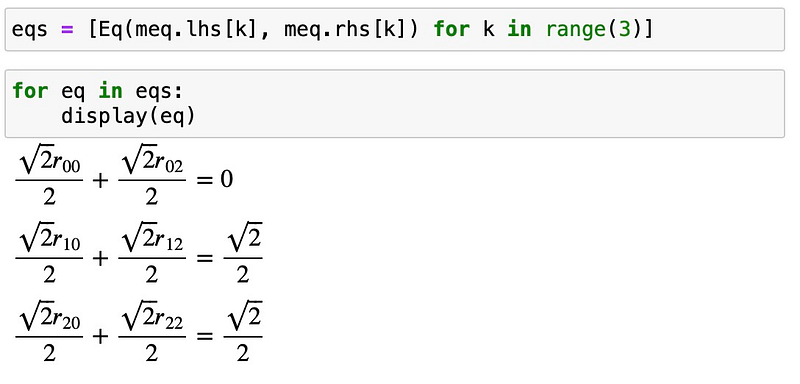
To complete the system, we require six additional equations. A useful fact is that the axis of rotation, which transforms A into B, must be orthogonal to both vectors A and B. Thus,
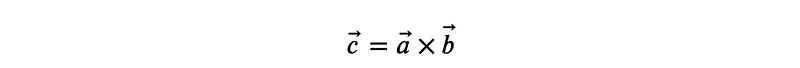
must remain unchanged during the transformation:
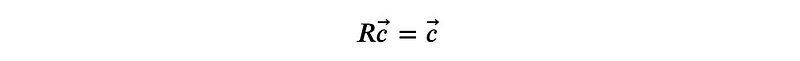

We can add this to our existing equations:
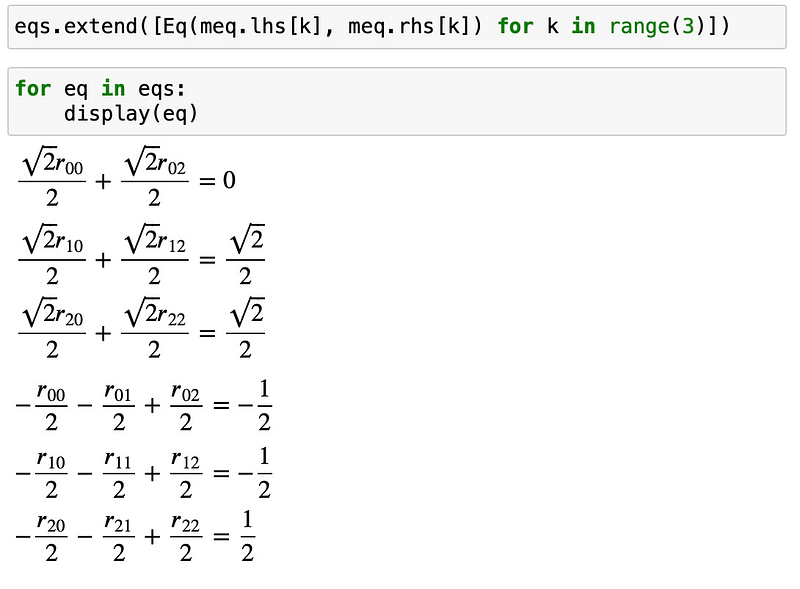
Now we have a total of six linear equations. We still need three more. It’s important to note that rotation matrices are orthogonal, meaning they adhere to the relationship:
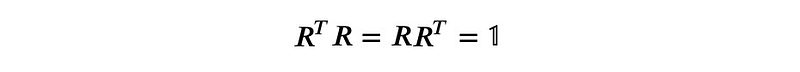
In SymPy, this is represented as:

These nine equations are nonlinear. We can simplify by taking three of the diagonal entries:
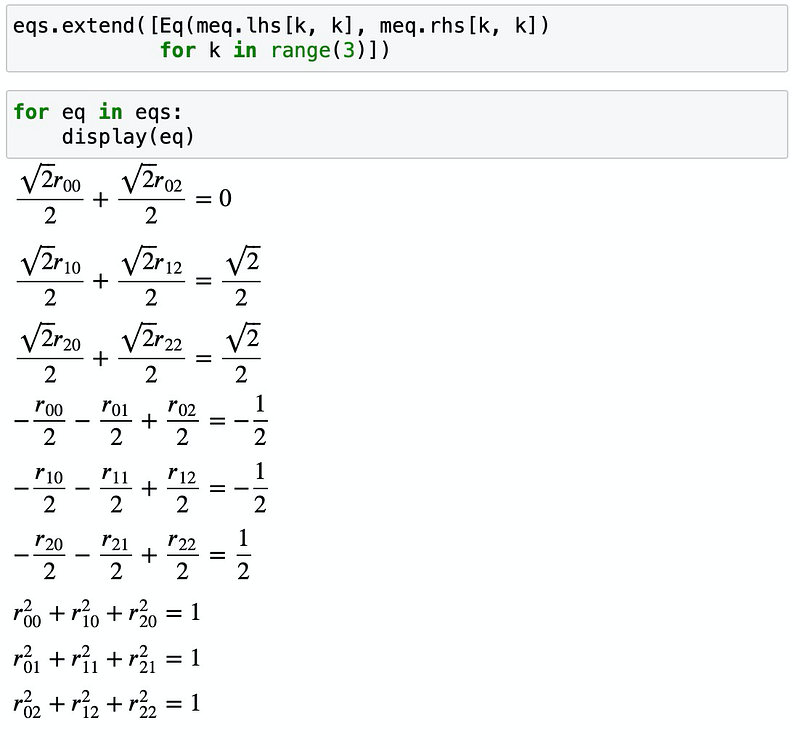
With these nine equations (ideally independent), we can proceed to solve the system. Note that by introducing three nonlinear equations, we may encounter multiple solutions. Fortunately, SymPy makes this process straightforward:

We find two possible solutions. To determine which one is valid, we can substitute them back into our equations:
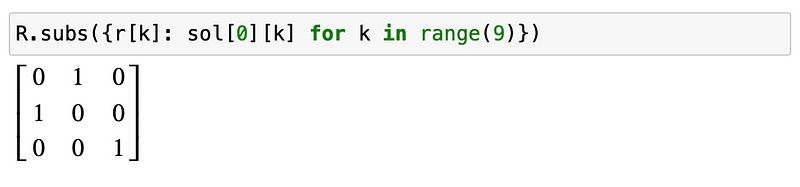
Analyzing the determinant provides insights into the nature of the solutions:

True rotations yield a determinant of 1, indicating that one of our solutions represents a rotation followed by a reflection. Let’s validate the other potential solution:
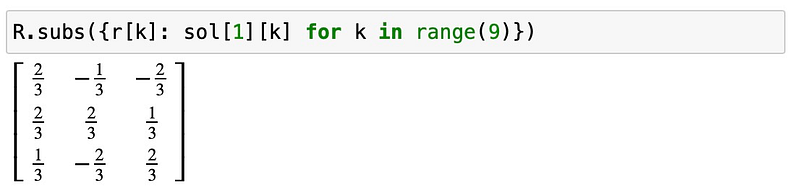

This solution aligns with our expectations and confirms our findings.
Chapter 2: Practical Applications of Rotation Matrices
In this video titled "Python: Sympy Matrices (Linear Algebra SOLVED!)", viewers will gain insights into the implementation of SymPy for solving linear algebra problems.
The second video, "Rotating a Vector with the Rotation Matrix", demonstrates practical applications of rotation matrices in vector transformations.