Chapter 1: Introduction to the Cube Dissection

Understanding how to visualize the dissection of a cube using planes can be quite challenging!

This intriguing problem was posed as the final challenge in the 2003 Australian Mathematics Competition (Intermediate Division). The question is as follows: For every vertex of a cube, a plane is drawn through the three neighboring vertices. How many sections do these eight planes create within the cube? Give it a shot; you might find it surprisingly difficult to conceptualize!

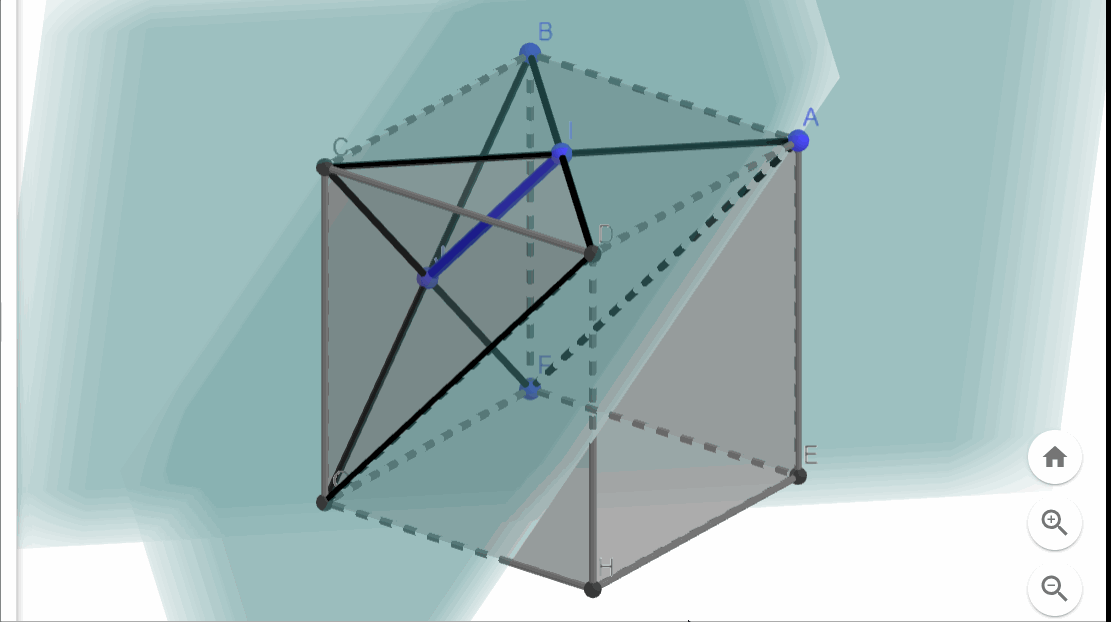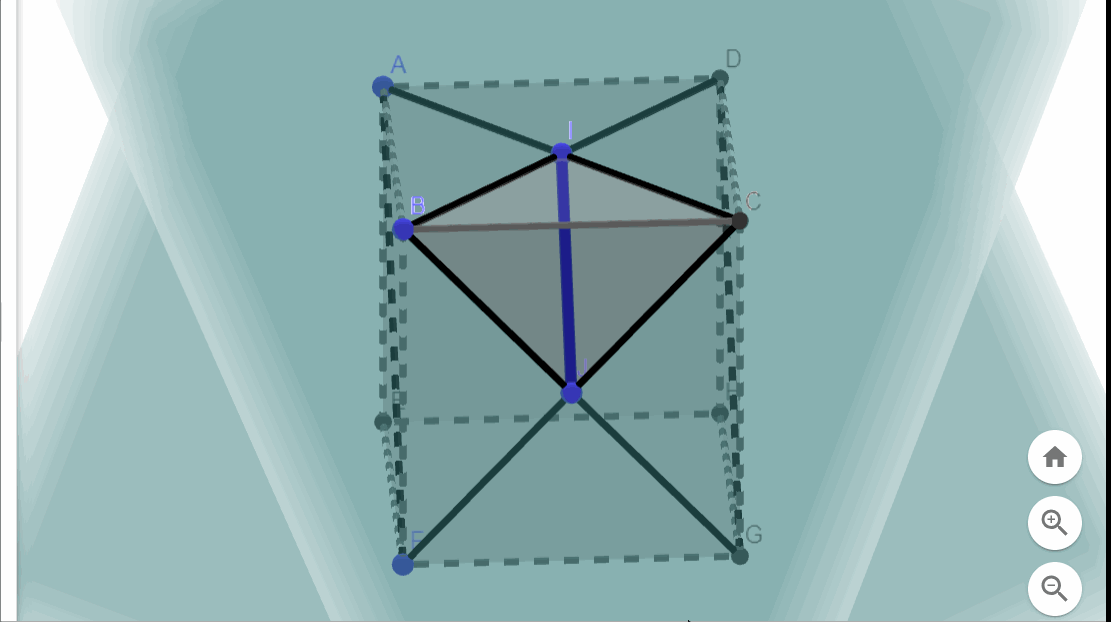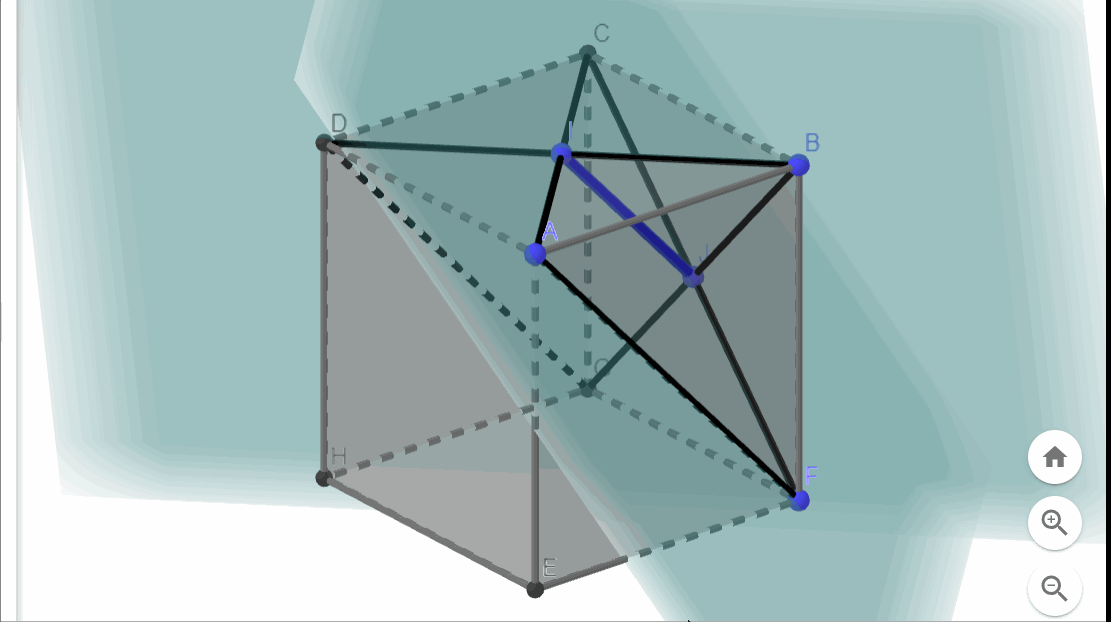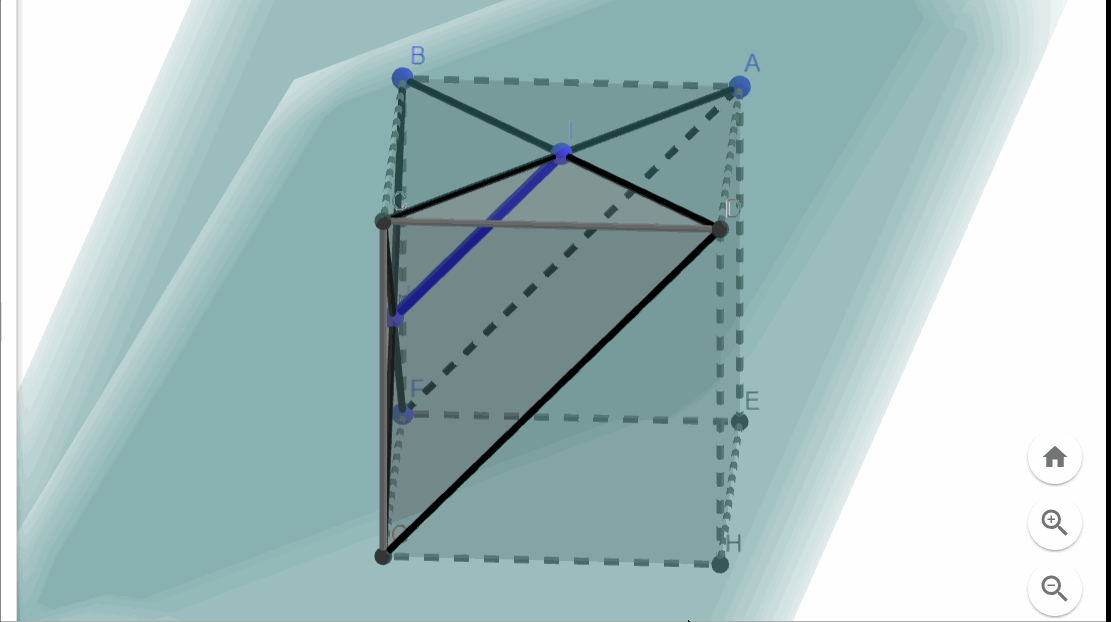
A crucial realization is that each plane intersects three of the cube's faces along their diagonals.

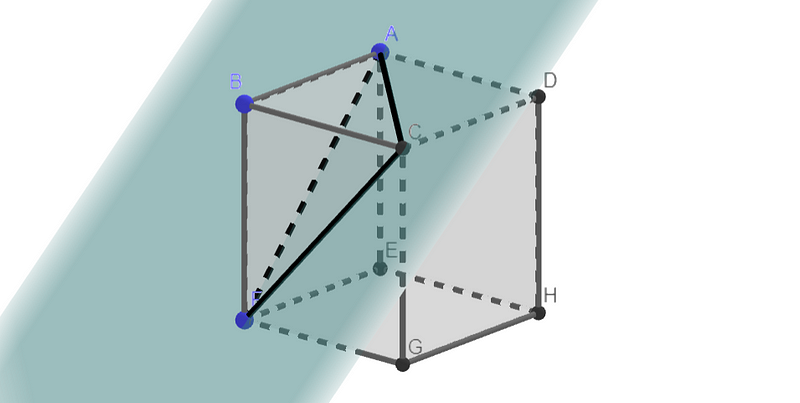
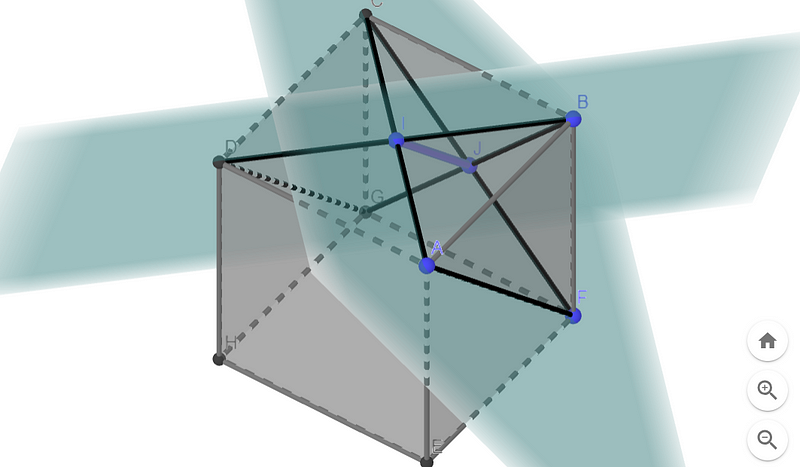
Indeed, there are two planes that intersect along each face's diagonal. Below, you can see two such intersecting planes.

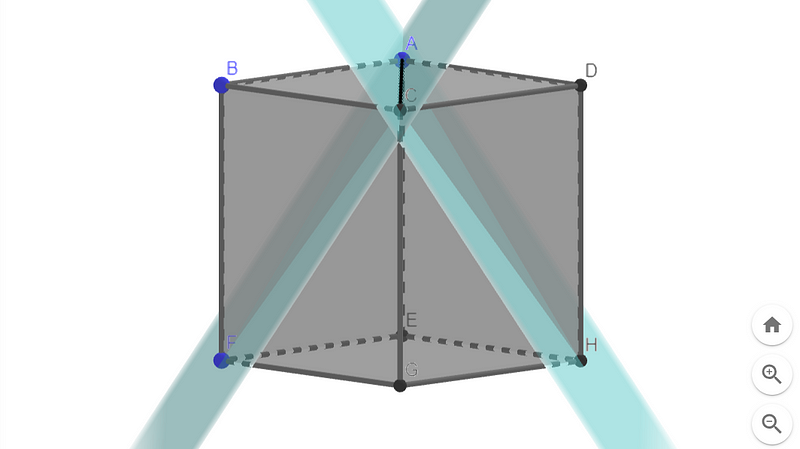
Next, let’s examine two planes that pass through the intersecting diagonals of one face.

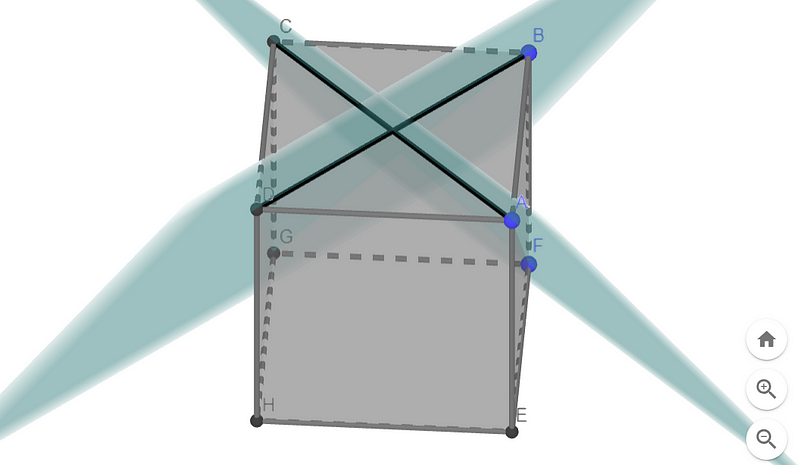
Visualizing the line where these two planes intersect can be more challenging. However, it is helpful to note that both planes extend through the centers of two adjacent faces. By connecting these two adjacent face centers with a line, we can identify the intersection line of the two planes.

An animation can clarify this concept further.

Due to the cube's symmetry and the arrangement of the eight planes, we will encounter eight similar intersection lines connecting each pair of adjacent face centers. This configuration results in an octahedron positioned at the cube's center.

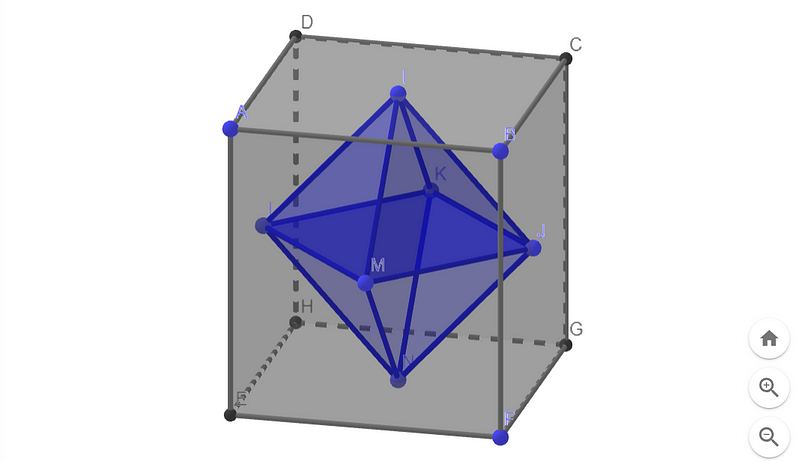
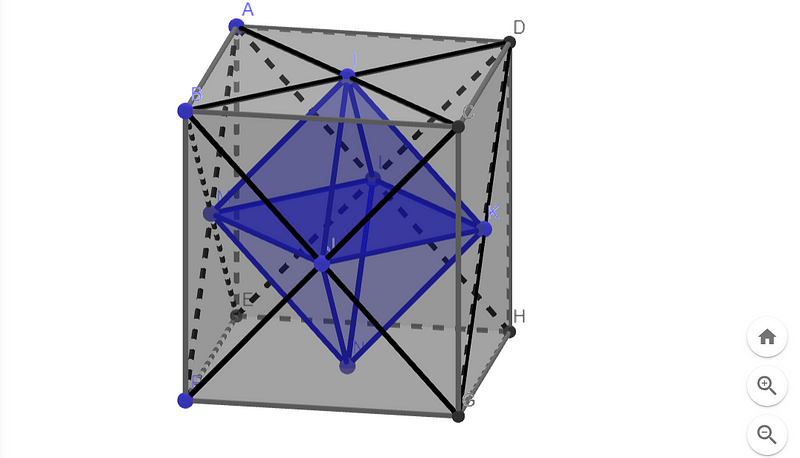
The eight faces of the octahedron correspond to the eight slicing planes. Fantastic! But what occurs outside this octahedron?

To answer this question, we need to reintroduce the face diagonals.

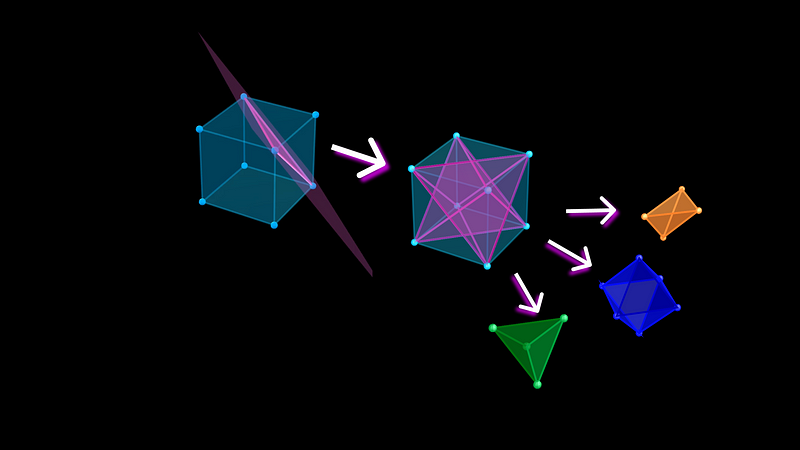
Let’s concentrate on a specific vertex of the cube. There are three face diagonals that connect this vertex to the three adjacent face centers, forming a tetrahedron (a triangular-based pyramid) with one of the octahedron's faces serving as its base (illustrated in green below).

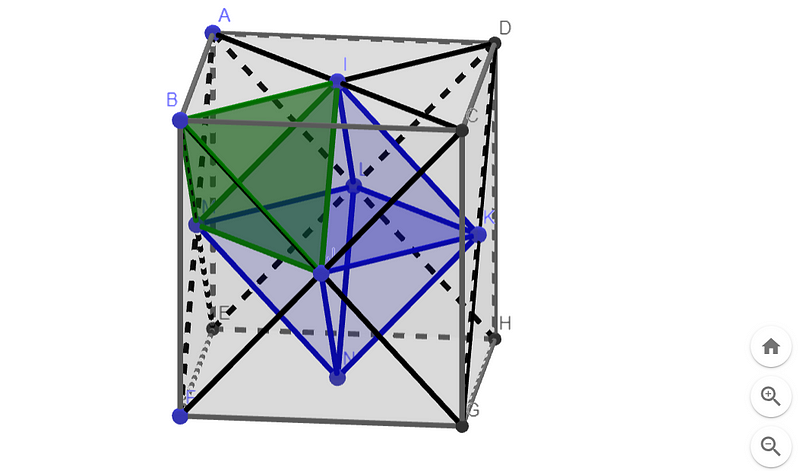
The three remaining faces of this tetrahedron divide the space surrounding the cube vertex into three additional regions. These too are tetrahedrons, albeit with a different shape from the green one. The tetrahedrons (illustrated in orange below) share a face with the green tetrahedron and an edge with the cube.

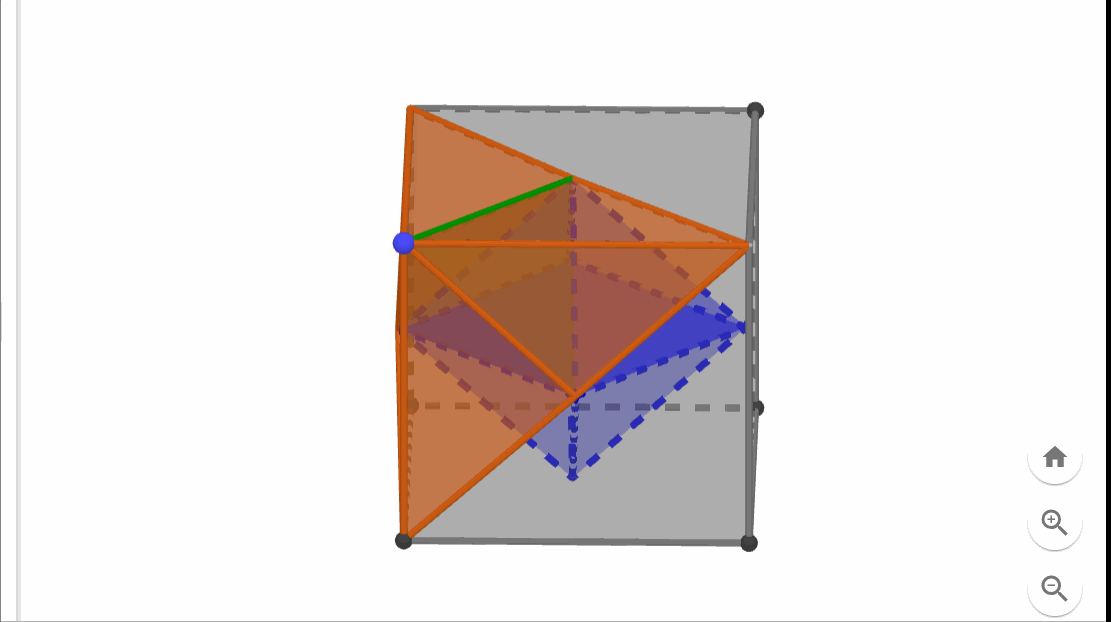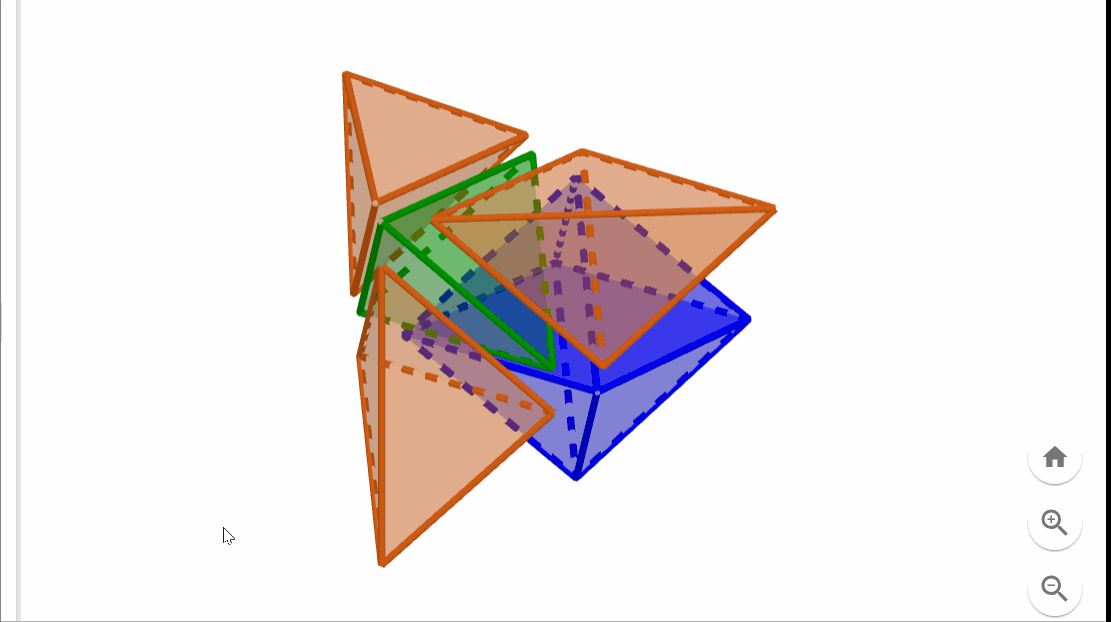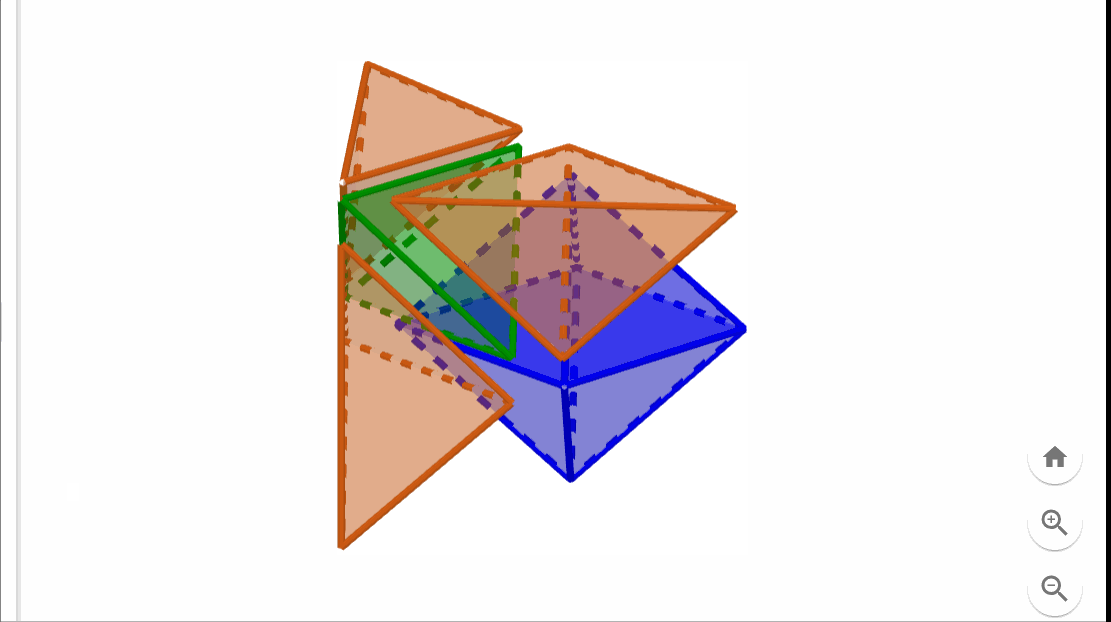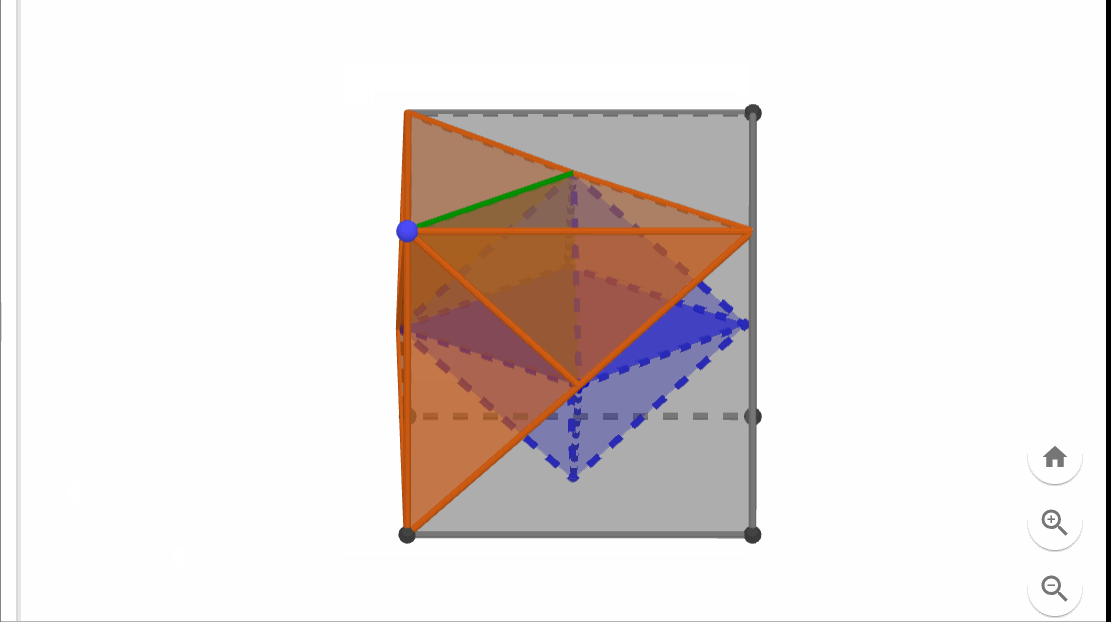
Now, let’s compile the overall picture. We have one (green) tetrahedron for each of the cube's eight vertices, an (orange) tetrahedron for each of the twelve cube edges, along with the (blue) octahedron at the center.

In total, this arrangement results in 21 distinct regions.