Understanding the Area of an Ellipse: A Comprehensive Guide
Written on
Chapter 1: Introduction to Ellipses
Ellipses are a crucial geometric figure in both mathematics and the natural world. Initially detailed by Menaechmus in the 4th century B.C., they have become a staple in mathematical curricula. Notably, in the 17th century, Johannes Kepler revealed that these shapes accurately describe planetary orbits. Essentially, an ellipse can be visualized as a circle that has been elongated in one direction. Before we delve into calculating the area of an ellipse, it’s important to clarify some terminology and fully grasp what an ellipse is.
Definition of an Ellipse
Ellipses are part of the conic sections, defined as the intersection of a plane with a cone at an angle.
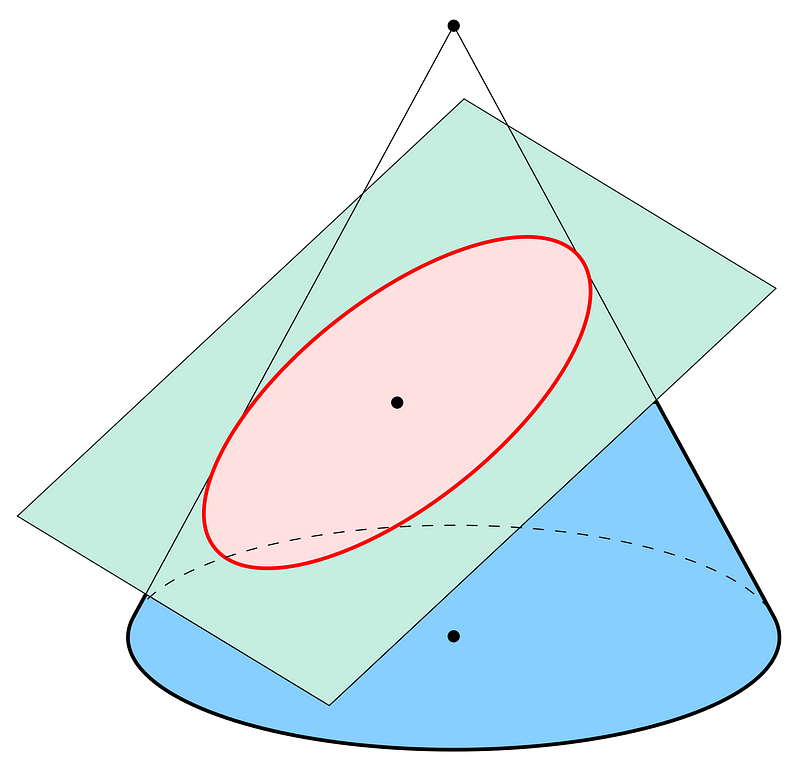
An ellipse is depicted in red. Source
An ellipse can also be characterized as a line where the sum of the distances from any point on the line to two fixed points, known as the foci, is constant. This definition may seem complex, so let’s break it down with a visual aid.
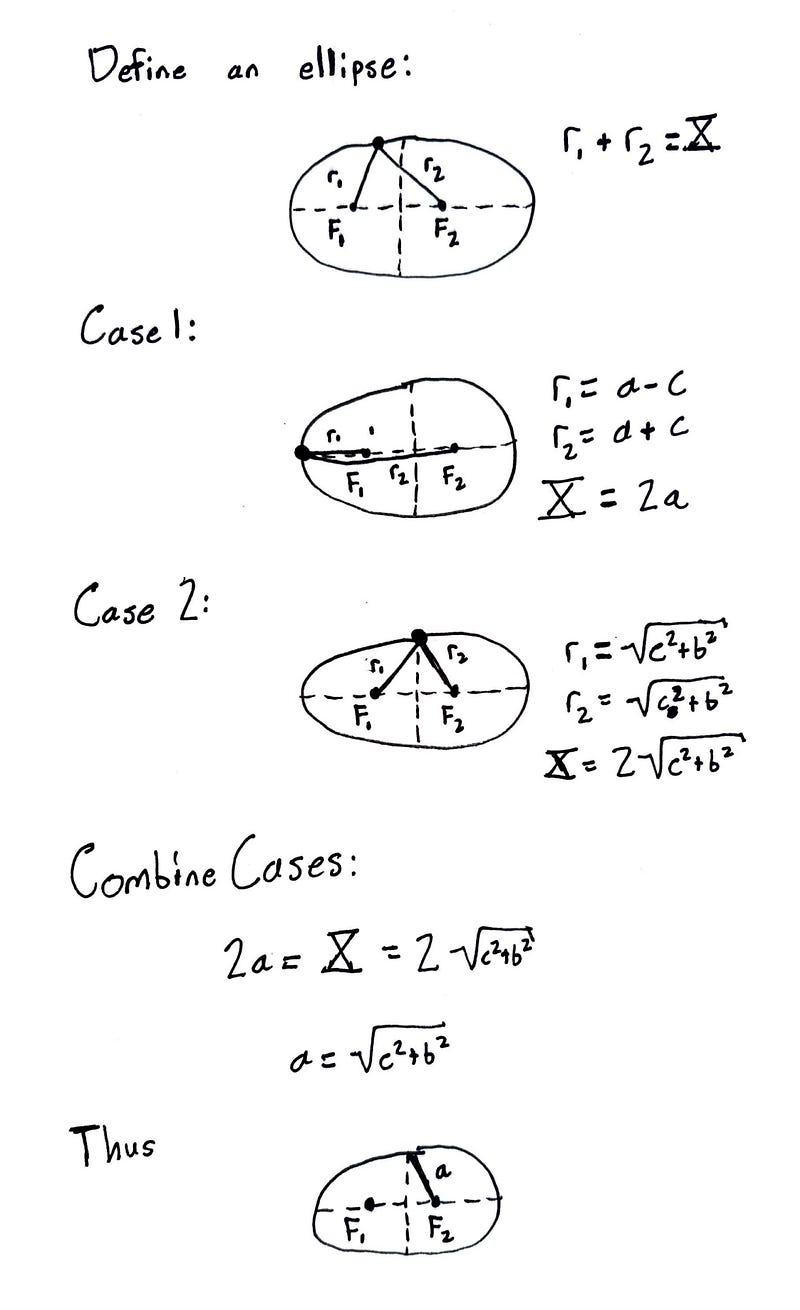
We begin with two fixed points, designated F1 and F2, which define the ellipse. We then establish a constant distance, labeled X. For every point A along the ellipse, the total distance from A to F1 plus the distance from A to F2 equals X.
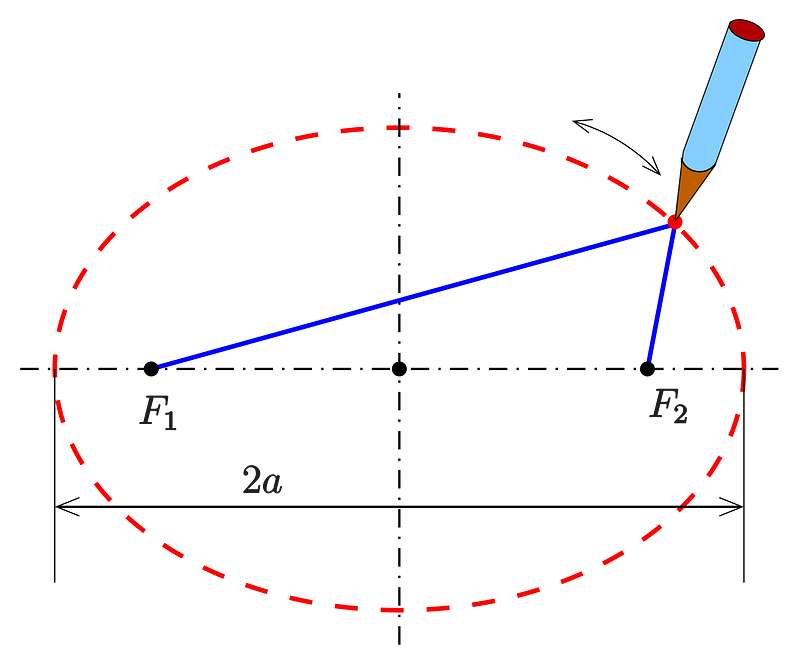
To draw an ellipse, you can use a string attached to the two foci. The length of the string corresponds to X. (Source)
Now that we’ve covered the fundamentals, let’s introduce a couple of additional lengths necessary for understanding an ellipse.
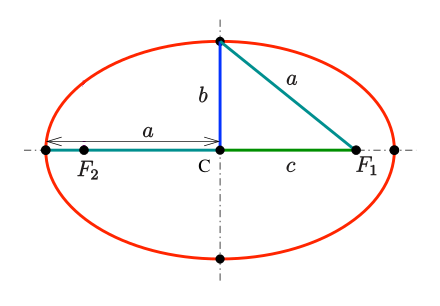
An ellipse features a semi-major axis, denoted as a, and a semi-minor axis, denoted as b. The semi-major axis is always longer and aligns with the two foci. There’s also the distance from the center of the ellipse to a focus point, referred to as c. It’s worth noting that the distance a appears twice: once as the distance from the center of the ellipse to the end of the semi-major axis and again as the distance from a focus point to the end of the semi-minor axis. Can you figure out why this holds true? A hint: employ the Pythagorean Theorem along with the initial definition of an ellipse; the answer is provided at the end of this article.
Another vital characteristic of an ellipse is its eccentricity, defined as the ratio of c to a. This can be represented as follows:
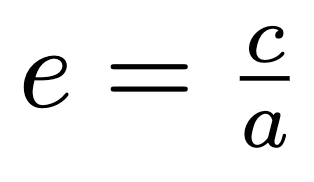
We can interpret eccentricity as a measure of how "stretched" an ellipse is. An ellipse with an eccentricity of 0 is simply a circle (where the foci coincide). A circle is thus a specific type of ellipse. Conversely, an ellipse with an eccentricity of 1 is infinitely stretched and resembles a straight line.
Chapter 2: Calculating the Area of an Ellipse
With the foundational definitions established, how do we determine the area of an ellipse? Recall that a circle is a particular instance of an ellipse, and we calculate its area using the following formula:
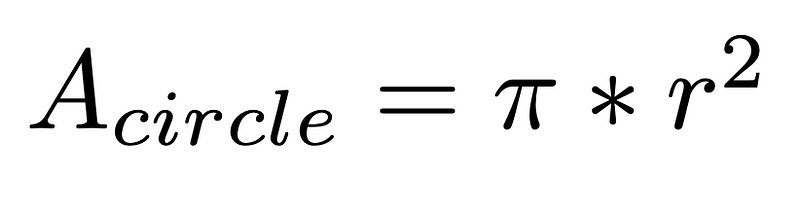
To adapt this for an ellipse, we need to consider the meanings of the values a and b, which represent the semi-major and semi-minor axes, respectively. This connection is the key step to finding the area of an ellipse.
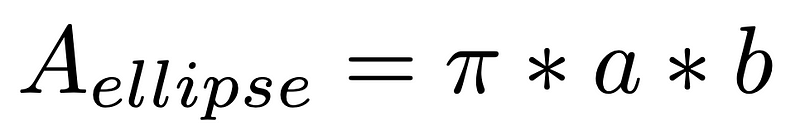
If you seek a detailed proof of this formula, I suggest checking the two proofs available. The first requires some calculus knowledge, while the second relies on geometric theorems and the relationship between ellipses and circles. Feel free to share which proof you prefer in the comments!
I hope you found this information enlightening! If you appreciate my work, consider becoming a Medium member through this link to support me! You can also follow me or my publication, Science Pathways, for more insightful articles—I publish weekly on topics in math and science.
Lastly, here is my handwritten proof demonstrating why the distance from a focus point to the end of the semi-minor axis equals a. This proof utilizes the distances a, b, and c as previously defined.