Chapter 1: The Birthday Paradox Unveiled

The concept of the birthday paradox is a captivating exploration of probability that reveals how likely it is for individuals in a small group to share the same birthday. Surprisingly, in a group of just 23 people, there is a 50% chance that at least two individuals have their birthdays on the same day, a fact that may seem counterintuitive given the 365 days in a year.

In this article, we will derive a formula that estimates the likelihood of shared birthdays across groups of different sizes. Let's dive in!

To start, we will skip the general formula for now and look at a specific example involving thirty individuals. First, we consider one person's birthday. When we introduce another person, the chances that they share a birthday with the first is 1 out of 365. As we add more people, the calculations become increasingly complex since we must evaluate each new person's birthday against those already considered. The most effective way to determine the probability of a shared birthday is by utilizing the classic method of probability calculation:

Written by me

In this context, P(Event) signifies the probability of a specific event occurring. The beauty of probability is that it can be boiled down to either happening or not happening. For instance, if there’s a 5% chance of your train being late, this translates to a 95% chance of it being on time. As we delve deeper into probability theory, let’s express these percentages as decimal probabilities: 5% becomes 0.05, and 95% converts to 0.95.

It’s far simpler to calculate the probability that no one in our group of thirty shares a birthday, meaning we need to find the likelihood that each individual has a unique birthday. The first person has no restrictions — they can celebrate on any day. Thus, P(No shared birthday) = 1. The second person now has one day less available to avoid a shared birthday:

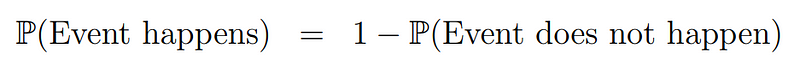
Written by me

The third individual now has two fewer options out of the total 365 days:

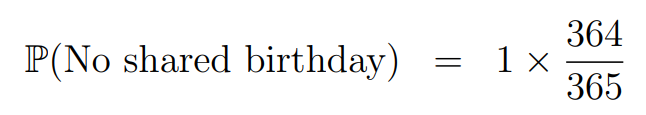
Written by me

Are you spotting the trend? Each successive individual has one less birthday option than the previous one, so by the time we reach the thirtieth person, they have 365–29 days available to choose from. Let's calculate the probability for thirty individuals:

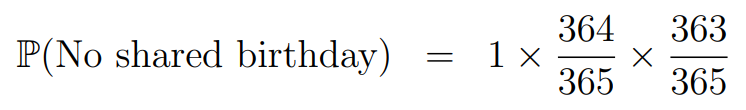
Written by me

The capital Pi notation indicates a product of all integer values of i ranging from 0 to 29. By applying our traditional method, we find that in a group of thirty:

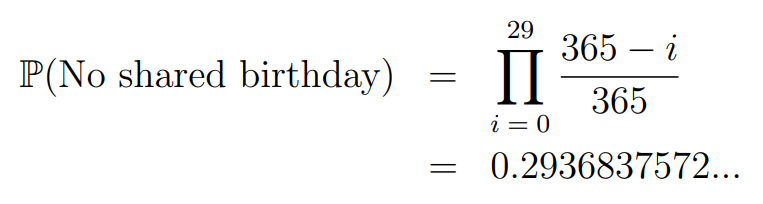
Written by me

The resulting probability is approximately 0.7, which translates to more than a 2/3 chance that at least two individuals in a group of thirty will share a birthday!

Armed with this understanding, we can now calculate the probability of shared birthdays for any size group. If we denote the number of people as n, we can adapt our previous calculation. For the thirty-person example, we calculated the product of thirty fractions, each with a denominator of 365 and a numerator decreasing by one for each new person. To generalize this for n individuals, we simply replace the 29 with n - 1:

Written by me

Once again, we use our traditional method:

Written by me

This is the elegant formula we sought! Note that it only applies for integer values of n ranging from 1 to 366. Let’s plug in some numbers to see what we uncover.

For a group of twenty people, the chance of a shared birthday is around 41%. In a group of fifty individuals, the probability skyrockets to 97%. Fifty is significantly fewer than the total number of days in a year!

What if we flip the question and ask how many individuals are needed to reach a 99% probability of a shared birthday? The answer is just 56 people.

For a 99.9% likelihood? Only 70 individuals are required. And for a staggering 99.99% chance, it takes 80 people.

Even with these calculations, this phenomenon can still feel unbelievable, which is why it earns the title of paradox.

Challenge: Utilize the formula to determine how many individuals are required for a 75% chance of a shared birthday. WolframAlpha can assist with calculations involving products. Simply navigate to the ‘math input’ section, found under calculus.

Chapter 2: Exploring the Birthday Paradox Further

This video titled "The Birthday Paradox" delves into the intriguing mathematical principles behind shared birthdays, providing a visual explanation that enhances understanding of the topic.

In this video, "The Birthday Paradox - Explained," the presenter further clarifies the concept and its implications, making the paradox accessible to all viewers.