Understanding the Raven Paradox: A Deep Dive into Scientific Reasoning
Written on
Chapter 1: Introduction to the Raven Paradox
The raven paradox challenges one of the essential elements of scientific inquiry: the nature of evidence. At its essence lies the inquiry:
“What constitutes evidence?”
In the 1940s, logician Carl Gustav Hempel introduced a thought-provoking logical puzzle to illustrate this paradox. He began with the assertion:
“All ravens are black.”
This statement serves as the foundation of the paradox's name. Imagine you're on a quest to determine the truth of this assertion.
Your journey leads you to encounter a black raven first. Naturally, you might view this as evidence supporting the original claim. Although it’s merely a single instance of a black raven, it provides some evidence in favor of the assertion.
Now, consider a green apple. Would you think this serves as evidence for or against the initial statement? Instinctively, you might find this information to be irrelevant. However, what if I told you that it actually supports the original assertion?

Illustration created by the author
This notion seems counter-intuitive and perhaps incorrect. Yet, this is the challenge posed by the raven paradox.
The Broader Question
The overarching question we need to address is:
“Can we develop a logical framework to evaluate evidence supporting or contradicting any given statement?”
In this discussion, I will simplify the paradox using an intuitive method that integrates three crucial components. We will steer clear of complex formalities to keep the analysis straightforward.
To grasp the challenge better, we should first explore four fundamental concepts that, despite their sophisticated names, describe straightforward ideas about human reasoning:
- Confirmation
- Instance Confirmation
- Equivalence Condition
- Contrapositive Statement
Don't let the terminology intimidate you; these concepts are quite accessible. Let’s begin with the idea of confirmation.
Section 1.1: The Concept of Confirmation
In fact, we have already touched upon confirmation earlier in this essay without explicitly defining it.
Consider a detective story: Suppose a detective investigates a crime and learns that the butler was present at the scene on the day it occurred. This information serves as evidence (not definitive proof!) for the theory that the butler committed the crime. This is what we mean by confirmation.
Later, it is revealed that the butler was not at the scene during the crime. The detective then considers this evidence as disconfirmation of the assertion that the butler committed the crime.
Additionally, if the detective discovers that a sandstorm occurred on Mars at the same time, she would regard this detail as irrelevant. This is what we define as a neutral statement—it neither confirms nor disconfirms the hypothesis.
Now that we’ve discussed confirmation, let's move on to instance confirmation.
Section 1.2: Instance Confirmation
To grasp instance confirmation, let’s revisit our original assertion:
“All ravens are black.”
This statement represents a general hypothesis. Instance confirmation implies that encountering a single example of the general hypothesis can serve as evidence supporting it.
In our case, seeing a black raven contributes some evidence affirming the hypothesis that all ravens are black.
With that concept clarified, let’s proceed to the equivalence condition.
Chapter 2: Exploring the Equivalence Condition
Let’s examine two statements that convey identical meanings, despite differing in phrasing:
- Statement A: Frozen water is entirely composed of ice.
- Statement B: Ice is what frozen water consists of entirely.
Though expressed differently, both statements communicate the same idea, making them equivalent.
The equivalence condition asserts that two equivalent statements must both be true or both be false. There cannot be a scenario where one is true and the other is false; that would create a contradiction.
Now, let’s move to the next essential concept: the contrapositive statement.
Section 2.1: The Contrapositive Statement
I must admit, the contrapositive statement is a more advanced concept and is rarely used in everyday situations. It is primarily relevant in scientific discussions within mathematics, logic, and philosophy.
The contrapositive statement expresses logical equivalence through negation. To illustrate, consider these two statements:
- Statement A: If it is raining, then the grass is wet.
- Statement B: If the grass is not wet, then it is not raining.
While these statements seem different, they essentially express the same logical meaning.
In general terms, the contrapositive statement follows this format:
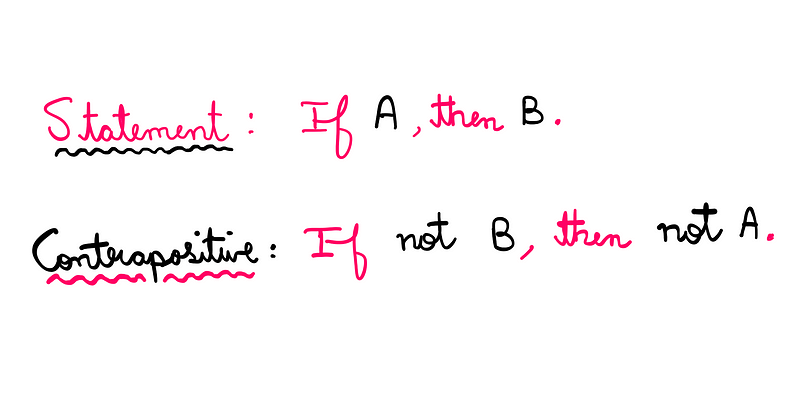
Image created by the author
Upon first encountering this concept in discrete mathematics, I found it challenging to fully comprehend. If you feel confused, that’s perfectly okay. Understanding the contrapositive statement is crucial to grasping the raven paradox.
Recognizing this principle will also enhance your ability to discern misinformation in real life, bolstering your logical reasoning skills.
Once you feel comfortable with the contrapositive, we can tackle the main issue at hand.
Chapter 3: Unraveling the Raven Paradox
Now, we will utilize everything we have learned to decode the raven paradox. Let’s return to our original assertion and reformulate its contrapositive:

Image created by the author
Although the contrapositive may appear to be an awkward rephrasing of the original assertion, it holds the same logical meaning, establishing their equivalence.
When you encounter a green apple, the original statement might seem irrelevant at first. However, when viewed through the lens of the contrapositive, the green apple serves as evidence supporting the original hypothesis (that all ravens are black).
The logic is sound: the green apple is neither black nor a raven, thus contributing to the confirmation of the original hypothesis.
To summarize our findings:
- We reformulated the original statement into its contrapositive form.
- We recognized that both statements are equivalent.
- By considering a non-related entity (the green apple), we confirmed the contrapositive statement.
- Consequently, this provides evidence for the original assertion.
Thus, we can confirm a hypothesis about ravens simply by observing a green apple or even a blue car. This may seem absurd, but it is logically consistent. This paradox reveals a conflict between inductive reasoning and intuition—the raven paradox!
Final Thoughts
Ultimately, we used logically coherent elements—instance confirmation, the equivalence condition, and the contrapositive statement—to arrive at a conclusion that appears logically inconsistent.
To make sense of this paradox, we must choose one of the following paths:
- One of the three concepts (instance confirmation, equivalence condition, or contrapositive statement) must be false.
- The conclusion does not logically follow from the valid components we assembled.
- The conclusion, although seemingly false intuitively, must be true.
How would you approach this dilemma? As you reflect on the implications of this paradox, remember that you are not alone in this inquiry. Scholars and philosophers have grappled with this challenge for decades.
In a forthcoming essay, I will explore potential methods for addressing the raven paradox!
Update: I've published a follow-up essay titled "How To Really Tackle The Raven Paradox?" for further insights.
References and credit: Carl Gustav Hempel (scientific paper) and Marc Lange (presentation).
If you appreciate my work, consider supporting me by clapping, following, and subscribing.
For further reading, you might find "The Thrilling Story Of Calculus" and "The Strong Law Of Small Numbers" intriguing.