Chapter 1: Understanding Digit Count

Calculators can certainly assist with number crunching, but let’s dive into a more intriguing question:

How many digits would the number ( 2023^{2^{23}} ) have if expressed in decimal form? My students possess a sophisticated calculator, but when tasked with evaluating ( 2023^{2^{23}} ), the results can be puzzling. Some calculators display “Error: overflow,” while others simply indicate the answer as “?.”

So, what can you do to tackle this challenge? A practical approach would be to calculate smaller powers of 2023 and identify any discernible patterns.

• ( 2023^2 = 4092529 ) (7 digits)
• ( 2023^3 = 8279186167 ) (10 digits)
• ( 2023^{2^{1}} = 1.675 times 10^{13} ) (14 digits)

Notice that moving from ( 2023^2 ) to ( 2023^3 ) results in a digit increase of 3, whereas the transition from ( 2023^3 ) to ( 2023^{2^{1}} ) shows an increase of 4 digits. One student cleverly used this trend to predict that the digit count for ( 2023^{2^{23}} ) might be approximately ( 2023 times 3.25 approx 6575 ).

That’s a commendable estimate! But how can we pinpoint the exact digit count?

Let’s simplify the problem by asking: how many digits are in ( 1000^{1^{3}} )? This scenario is easier since the base is a power of 10. We know:

• ( 10^2 = 100 ) has 3 digits,
• ( 10^3 = 1000 ) has 4 digits,
• ( 10^4 = 10000 ) has 5 digits, and so forth.

Thus, ( 1000^{1^{3}} ), which can be rewritten as ( (10^3)^{1^{3}} = 10^{3^{3}} ), must contain 3001 digits.

But how does this insight assist with ( 2023^{2^{23}} )? What mathematical operation can help us determine the necessary power of 10 for any number?

The answer lies in the base 10 logarithm! Those who studied mathematics before the advent of calculators would likely find this concept straightforward. However, my Year 10 Advanced Mathematics students found it rather challenging!

To evaluate ( log_{10}(2023^{2^{23}}) ) is our next step. While calculators may struggle with that, we can leverage another fascinating property of logarithms:

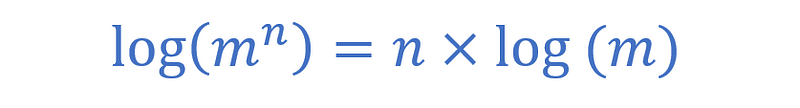
This logarithmic law stems from the multiplication of powers principle:

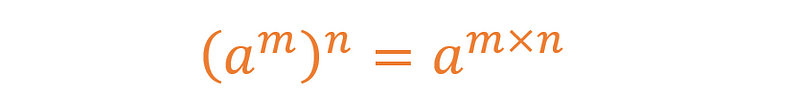
Thus, we can express the digit count as:

[

log_{10}(2023^{2^{23}}) = 2023 times log_{10}(2023)

]

A standard scientific calculator can evaluate this to approximately 6688.03. Consequently, the total number of digits is 6689. 🎉

Feel free to share this with your friends and family! I suspect those over 50 might grasp it quickly, while younger individuals might find themselves limited by their calculators!

This is a new Medium publication!

(started November 2022)

Explore other engaging math problems published thus far, and consider following the publication for more intriguing content. 🎉

Chapter 2: Videos on Digit Count

The first video explores the question, "How many digits are in the number ( 2^{1024} )?" - a fascinating dive into the world of large powers.

This second video asks, "How many digits does ( 3^{100} ) have?" - shedding light on the concept of digit counting in exponential terms.