Chapter 1: Introduction to Symmetries

How can we integrate smooth symmetries into particle models? In the realm of physics, we encounter a rich variety of symmetries that characterize our universe. These include symmetries that lead to the formation of particles, those that govern electromagnetic laws, and symmetries that arise from intricate systems. Mathematicians are often compelled to categorize these diverse symmetries to bring clarity to this complex landscape.

To begin, we might differentiate symmetries based on whether they are discrete or continuous. Discrete symmetries involve transformations that are abrupt, such as reflections across a specific axis. In contrast, continuous symmetries involve smooth transformations like rotations. For instance, the image below illustrates a reflection along the vertical axis of a square, demonstrating that a reflection is not a continuous transformation, whereas rotations are classified as continuous.

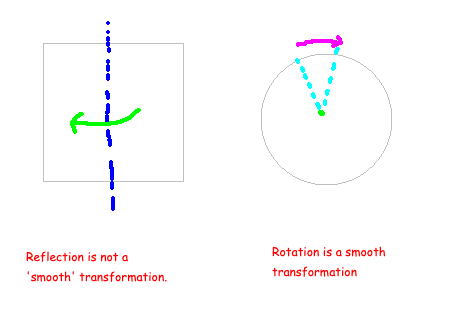
Continuous symmetries are particularly intriguing due to their desirable properties, often linked to geometrical shapes. Consider rotational symmetry, which can be defined by the degrees through which an object can be rotated, naturally associating this transformation with circular shapes. This leads us to the concept of manifolds, where such symmetries can be represented mathematically.

This brings us to Lie groups, which are mathematical constructs that encapsulate smooth transformations. The symmetry group for rotations serves as a prime example of a Lie group since rotation is a smooth transformation. Unlike reflections, which lack this smoothness property, rotations allow for infinitesimal adjustments.

Mathematical diagrams, often referred to as 'node and arrow' diagrams, are utilized to visually represent Lie algebras. Within this framework, a category of Lie groups known as semi-simple Lie groups has been classified into several distinct families. Notably, all finite semi-simple Lie algebras can be grouped into four infinite families designated as An, Bn, Cn, and Dn, along with five exceptional cases: E6, E7, E8, G2, and G4. This classification system is known as the Cartan classification for Lie algebras.

Chapter 2: Phase Rotations and Sigma Models

The video titled "Sigma models and Lie bialgebroids - Miquel Cueca - YouTube" delves into the intricate relationship between sigma models and Lie bialgebroids, providing insights into their mathematical foundations and applications.

What constitutes a phase rotation? Typically, a physical system is articulated using a mathematical expression known as a Lagrangian, which is often composed of the system's kinetic and potential energies. The Lagrangian may exhibit symmetry when the system undergoes a transformation. For instance, if the potential is cylindrical or funnel-shaped, it may maintain rotational symmetry. In high-energy systems, the symmetry of the Lagrangian is frequently preserved.

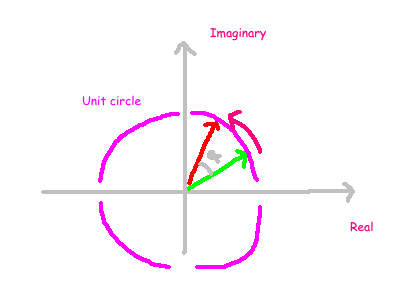
The simplest model exhibiting a 'smooth' symmetry is a phase rotation. This occurs when a field is multiplied by a complex number of unit length. A field is understood as a physical entity that holds a value at every spatial and temporal point. When applying a phase rotation, the field's 'imaginary' and 'complex' proportions are altered.

The philosophical implications of phase rotation remain a contentious topic among physicists and philosophers. This specific transformation is known as the U(1) group, with the '1' indicating that it can be represented by a single number.

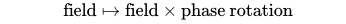
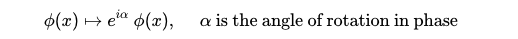
In the equation above, the Greek letter phi indicates the value of the field, while the exponential factor signifies the phase rotation. Additionally, we must consider how to apply this phase rotation to physical entities. This can be done in two ways: applying varying degrees of rotation across different field points, or maintaining a uniform rotation throughout the field. The former is termed local symmetry, while the latter is referred to as global symmetry.

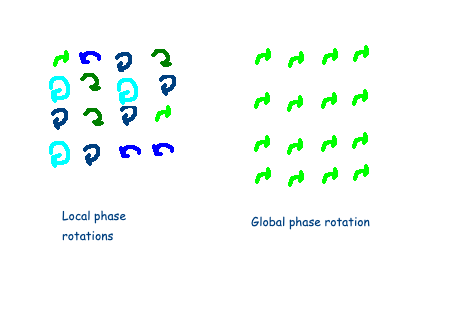
What are sigma models? The most straightforward Lagrangian embodying global phase rotation symmetry is found within a family of models known as sigma models. These models describe the dynamics of a complex-valued field, where each point in spacetime corresponds to a complex number. Sigma models are particularly noteworthy because they relate to Lie groups, such as U(1). The structure of the Lagrangian may appear complex, but it is often visualized as resembling a Mexican sombrero.

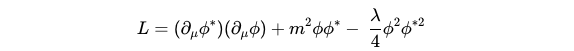
The Lagrangian comprises a kinetic energy term—where the star denotes the 'complex conjugate'—alongside a mass term and an interaction term. The final two components are often referred to as the 'potential' of the Lagrangian. An essential aspect of this Lagrangian is its invariance under phase rotations, indicating that it possesses U(1) symmetry.

The points at which the field exhibits no kinetic energy are termed 'stationary points.' These points signify a state of balance within the field. In classical physics, the equilibrium point typically corresponds to minimized potential values. These states can be either stable or unstable. Under certain conditions, such as low temperatures, a negative mass term may arise, leading to stable states existing within the sombrero's well. This scenario results in an infinite number of states classified as ground states, as each corresponds to a unique angle within this potential landscape.

The process of selecting a particular stationary point is referred to as symmetry breaking, a topic I have previously explored in detail.

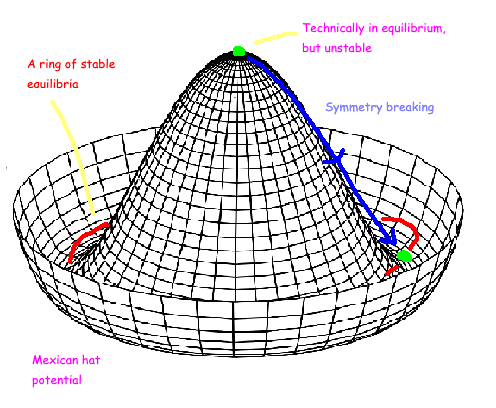
Why are stable states significant? Stable states represent conditions where a physical system remains in equilibrium, allowing it to reside without undergoing drastic changes. Moreover, these states are crucial because even minor disturbances (referred to scientifically as perturbations) will typically return to a stable condition. This concept can be likened to a particle resting at the bottom of a bowl; it remains in equilibrium and stable, even when subjected to slight perturbations. Conversely, if the bowl were inverted, the particle could be balanced yet would be sensitive to minute nudges.

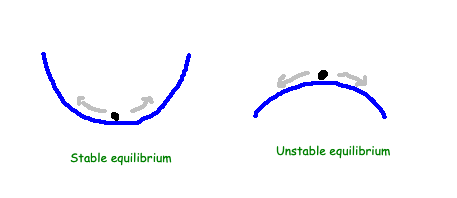
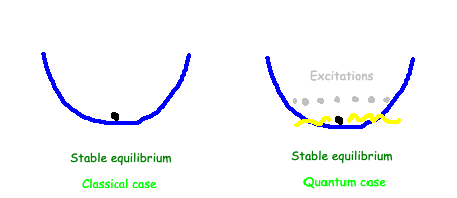
In the classical domains governed by Newton and Maxwell, we can derive straightforward conclusions concerning equilibrium points. For instance, according to the Euler-Lagrange equations, the field will correspond directly to the equilibrium value. Should the equilibrium occur at a field value of 1, the field will remain at this constant value over time, suggesting that it will settle into this steady ground state unambiguously.

However, in quantum mechanics, the situation is more nuanced. Fields exhibit probabilistic behavior and small fluctuations around the stationary state. By employing the Feynman path integral method, one can observe how these fluctuations influence physical phenomena. These excitations lead to intriguing physics, including the emergence of both massless and massive particles, a topic I will address in my forthcoming post!

Chapter 3: The Relevance of Lie Theory

The video titled "Why study Lie theory? | Lie groups, algebras, brackets #1 - YouTube" emphasizes the importance of Lie theory in understanding symmetry and its applications across various domains in physics and mathematics.