Exploring the Magic of the Pythagorean Theorem
Written on
Chapter 1: The Appeal of the Pythagorean Theorem
Teaching the Pythagorean Theorem has always been a highlight of my 8th-grade math curriculum. Interestingly, students often find it enjoyable, even those who generally struggle with math.
Why Students Enjoy the Pythagorean Theorem
The appeal of the Pythagorean Theorem can be attributed to several factors:
- It has a catchy name.
- The formula is simple and easy to recall.
- The math involved is quite straightforward.
- Typically, all students begin with a similar foundation, as there is little prerequisite knowledge needed compared to other mathematical topics.
Students quickly engage with problems, using their calculators to compute squares and square roots, which fosters a sense of achievement in mastering this concept. But what makes the Pythagorean Theorem so universally applicable?
Its effectiveness can seem almost magical, providing accurate results for every right triangle in our Euclidean framework. Is this phenomenon simply coincidental?
I find that exploring the theorem's proofs can be just as exciting as solving its equations, so let’s examine one of the most renowned proofs.

Chapter 2: Visualizing the Pythagorean Theorem
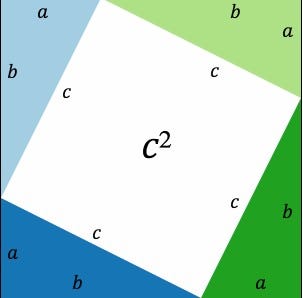
The Pythagorean Theorem is often best understood through visual aids, particularly because the formula involves squares, which denote area.
In the image displayed, four identical right triangles are arranged to form a square, a configuration that works regardless of the side lengths of the triangles.
The Hypotenuse Squared
The center white area represents (c^2), the square of the hypotenuse. All four sides of the central square measure (c), and it can be confirmed that the angles are right angles, thus verifying that it is indeed a square rather than a rhombus.
This verification stems from the fact that each corner of the white square is formed by the two acute angles of the green and blue right triangles. Since the angles of a right triangle always sum to 90°, and the straight line it rests on equals 180°, we have 180° - 90° = 90°. Therefore, the inner shape must be a square, as it possesses four right angles and four equal sides of length (c), leading to an area of (c^2).
Now, let's examine the next image.
The Sum of Squares
By repositioning the right triangles to form two rectangles, we create space for two white squares, whose areas are (a^2) and (b^2), reflecting the side lengths of the right triangles. This arrangement holds true for any set of four identical right triangles.
Putting It All Together
So, how does this demonstrate that (a^2 + b^2 = c^2)?
The repositioning of the blue and green triangles alters their arrangement without changing their area. Since the overall size of the larger square remains constant, the area of the white space in the left image ((c^2)) corresponds to the combined area of the two smaller white squares in the right image ((a^2 + b^2)).
In both configurations:
- White space + blue and green triangles = larger square
Given that both the larger square and the blue and green triangles maintain their dimensions, the white space in both images must be equivalent.
What to Do with This Information?
For educators, this serves as an excellent hands-on activity to demonstrate the theorem's validity. Students can cut out four identical right triangles of varying sizes, illustrating that the theorem applies universally to all right triangles. This also provides a clear contrast with non-right triangles.
I recommend teaching the formula first, allowing students to become comfortable with it, as they often find it easy to grasp. This initial success can boost their confidence and enhance their interest in exploring the proof.
Understanding this proof is not only engaging but also reinforces that mathematics is grounded in reality. By bridging algebra and geometry, we illustrate that math serves as a language governing our world.
Remember, numerous proofs exist for the Pythagorean Theorem. Explore different methods and find the one that resonates with you!
Discover the reasoning behind the Pythagorean Theorem in this enlightening video that explores why a² + b² = c².
Learn how to apply the Pythagorean Theorem with practical examples in this instructional video.