Chapter 1: Unveiling the Golden Ratio

This article delves into a fascinating problem inspired by the 2023 American Mathematics Competition, revolving around the folding of a paper pentagon.

A regular pentagon with an area of (1 + sqrt{5}) is printed on paper and cut out. When the five vertices of the pentagon are folded into the center, a smaller pentagon is formed. The question then arises: what is the area of this new pentagon?

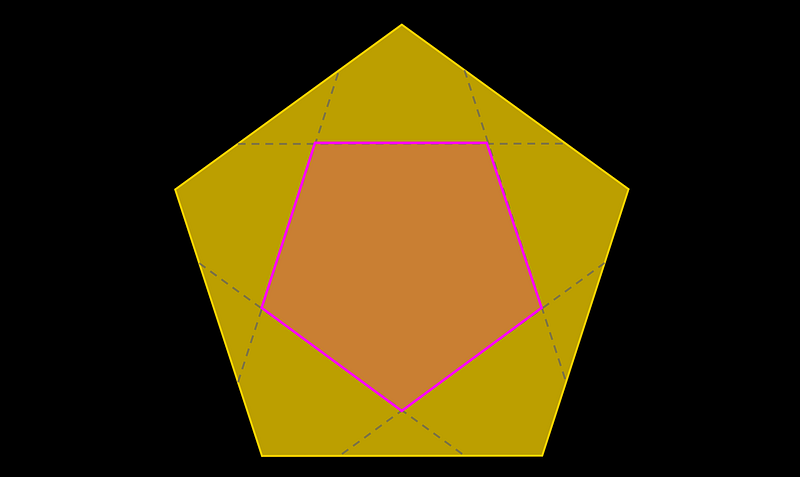
Feel free to attempt solving this problem before proceeding. Grab a pen and paper—it’s a fun challenge! There are numerous approaches to tackle it, many of which involve trigonometry with angles measuring (36^circ), (54^circ), or (72^circ).

One method I stumbled upon eventually led me to derive an expression for the ratio between the side lengths of the two pentagons: (2tan(54^circ)cos(54^circ)). While my calculations may not be entirely straightforward, the focus of this article lies elsewhere!

What caught me off guard about this result is that the expression (2tan(54^circ)cos(54^circ)) reveals itself to be none other than the golden ratio!

Upon this discovery (with a little help from my calculator), I became eager to find a more elegant way to illustrate the golden ratio's presence. But first, let’s take a step back.

Section 1.1: Understanding the Golden Rectangle

The golden ratio, often denoted as (phi), is frequently introduced through the concept of the golden rectangle. This rectangle maintains a ratio of (phi) between its sides, and a fascinating property arises: when a square is removed from one side, the remaining rectangle is similar to the original.

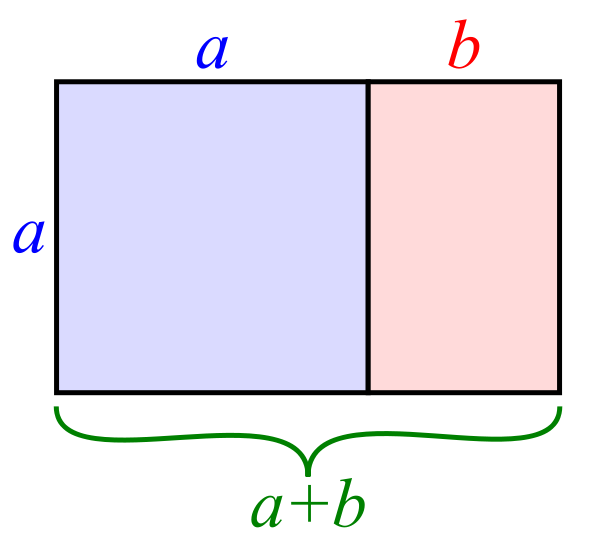
In the above rectangles, the ratios (a/b) and ((a+b)/a) both equate to (phi). The value of (phi) is derived from the positive solution to the equation:

[phi^2 = phi + 1,]

which results from rearranging the ratios.

Using the quadratic formula, we find that (phi = frac{1 + sqrt{5}}{2}). This golden rectangle has been utilized by renowned artists like Leonardo da Vinci and Michelangelo, as it is thought to embody a natural aesthetic appeal.

Section 1.2: The Golden Triangle

Less familiar than the golden rectangle is the golden triangle, an isosceles triangle where the two equal sides are (phi) times longer than the base. This triangle features two angles of (72^circ) and one angle of (36^circ), linking it closely to the regular pentagon, as established by Euclid.

One of Euclid’s most beautiful constructions involves inscribing a regular pentagon within a circle. Understanding this construction provides insight into the essence of the first four books of Euclidean geometry. — Kathryn Mann

The golden triangle can be visualized within the regular pentagon, where connecting the vertices creates a five-pointed star (the pentagram).

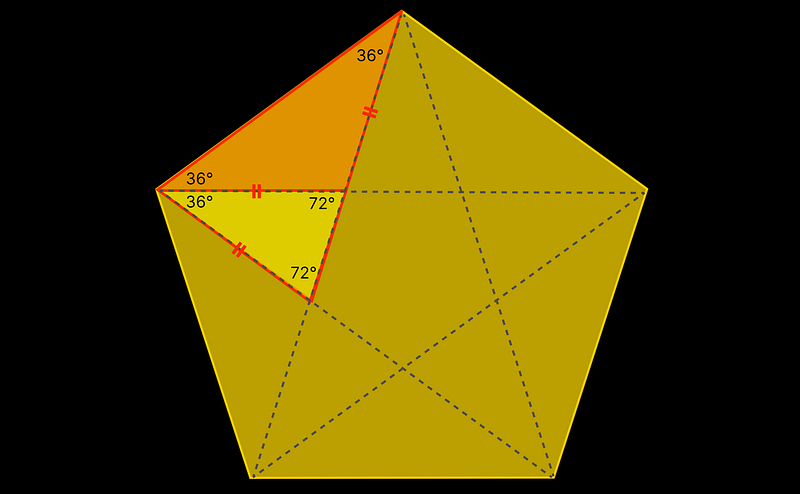
Just like the golden rectangle, the golden triangle contains a similar triangle within it. This similarity arises because (72^circ) is double (36^circ), or can be inferred from the equal side lengths of the pentagram.

The ratios between (a) and (b) in these similar triangles lead us back to the quadratic equation (phi^2 = phi + 1), yielding (phi = frac{1 + sqrt{5}}{2}).

Chapter 2: Locating the Golden Triangle

In a trigonometric exploration, I discovered that the length ratio between the folded smaller pentagon and the larger one is indeed (phi). But where exactly is the golden triangle concealed?

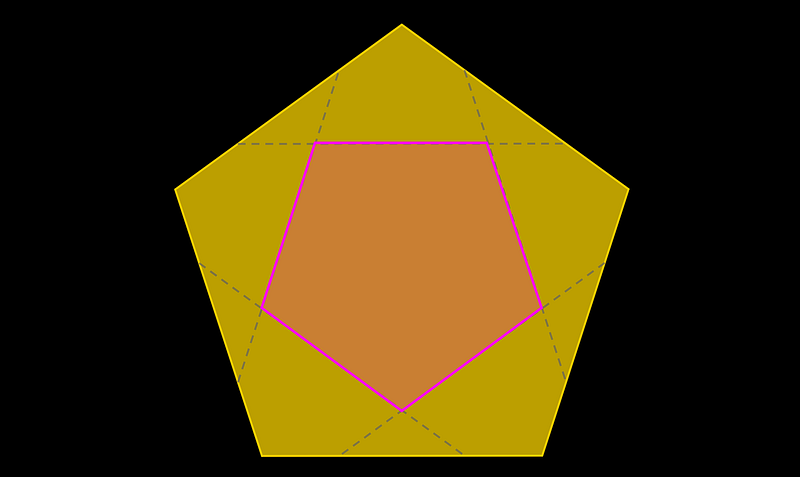
I spent considerable time searching for it and won’t delve into all the tangents I explored along the way! However, the simplest way to recognize it is as follows:

When a vertex is folded to the center, it creates an isosceles triangle with angles of (36^circ) and (108^circ).

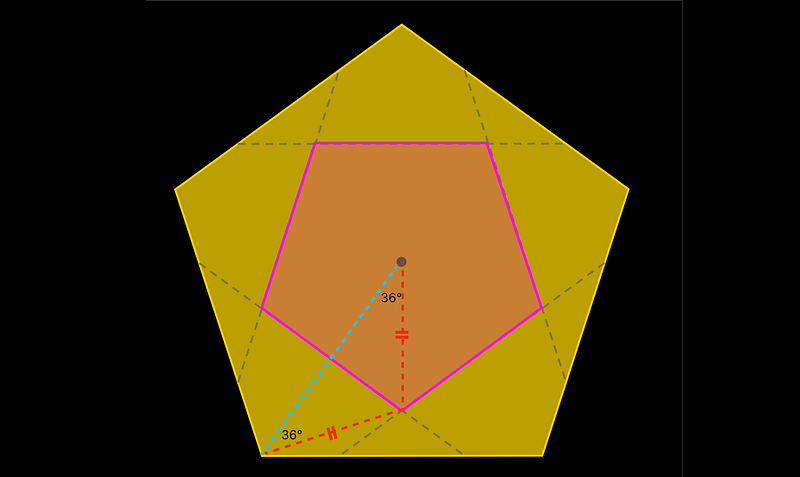
To clarify, let's add the smaller golden triangle at the bottom to complete our visual.

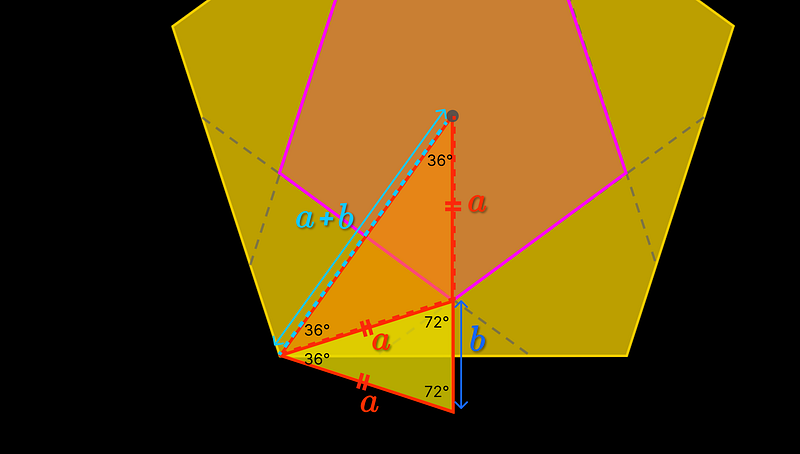
The distance from the center to the vertex of the smaller pink pentagon is (a), while the distance from the center to the vertex of the larger pentagon is (a + b). Since we are dealing with a golden triangle, this ratio ((a + b)/a) equals (phi = frac{1 + sqrt{5}}{2}).

It seems quite evident now, but it took me a while to uncover it, making the realization all the more fulfilling!

In this video, "The Math Hiding in Plain Sight," we explore the hidden mathematics of the golden ratio within geometric figures.

"Beyond Metatron's Cube: The Golden Fruit of Life" reveals breakthrough discoveries about the connections between geometry and the golden ratio.