Chapter 1: The Essence of Integration

To achieve proficiency in integration, one often needs to rely on experience. Many integrals necessitate knowledge of specific substitutions, recognition of symmetries, or simply familiarity with similar problems. This background enables us to quickly identify strategies, such as manipulating fractions or cleverly adjusting terms to achieve a desired result. A prime example of the importance of experience can be illustrated through the integral we will tackle together.

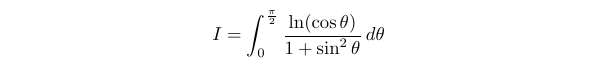
At first glance, this integral may appear daunting; it features cosine terms nested within a logarithmic function, and no clear substitution is evident. This is where our experience becomes crucial, as determining the starting point often demands significant contemplation.

A useful approach when encountering trigonometric functions is to transform them into tangent and sec² forms. This method can pave the way for advantageous substitutions using t = tan(θ), given that the derivative of tan(θ) is sec²(θ), which we will explore shortly. So, how do we initiate this integral with this strategy in mind? One possibility is to multiply both the numerator and denominator of our fraction by sec²(θ).

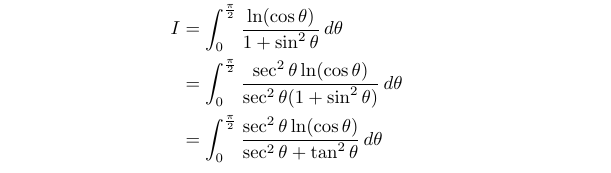
Now, we will apply the substitution t = tan(θ). This requires us to express cos(θ) in terms of tan(θ), which involves some straightforward algebraic manipulation.

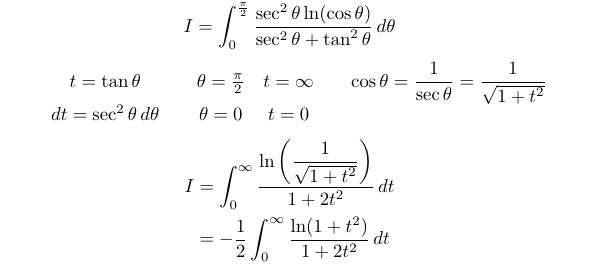
You might be asking how this transformation has assisted us. The current form of the integrand is guiding us toward Feynman’s technique, which is frequently employed in these scenarios. If you’re unfamiliar with this method, I will explain it in this article, highlighting its effectiveness in these types of integrals.

Feynman’s technique enables us to evaluate integrals like the one at hand by utilizing the principle of ‘differentiating under the integral sign’. Feynman first encountered this method while studying Frederick S. Woods' Advanced Calculus.

We will now implement this technique for our integral. Knowing where to introduce our parameter in the integrand is also a skill that comes with practice. For this integrand, the most common placement for the parameter is within the logarithmic function, as ln(1 + θt²). Let’s give this a try!

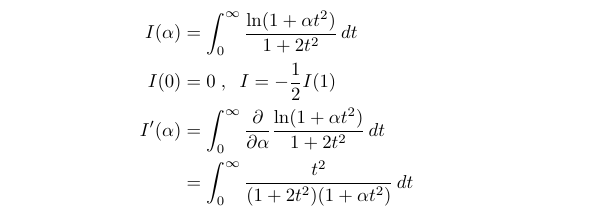
Next, we will conduct a partial fraction decomposition, allowing us to proceed with the integration.

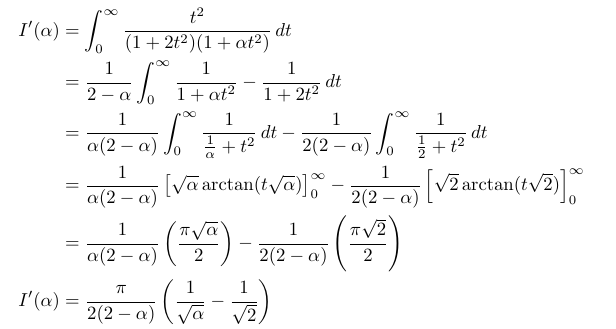
Subsequently, we must integrate with respect to θ, keeping in mind that we will obtain a constant of integration, which we can solve for using the fact that I(0) = 0.

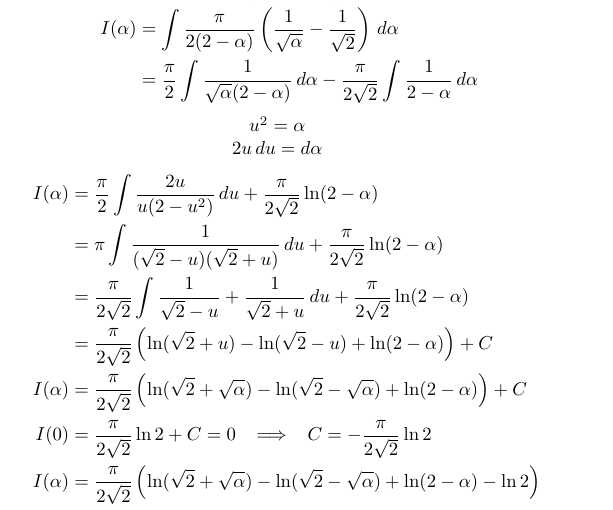
Fantastic! Now, we just need to compute I(1).

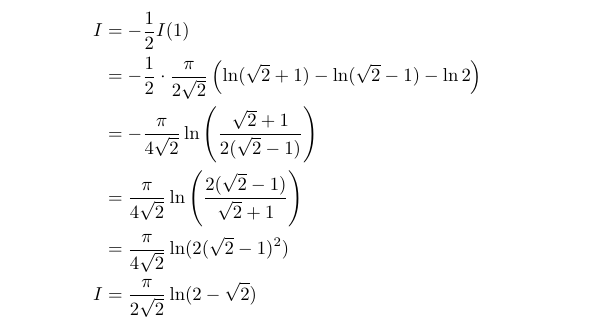
What an impressive outcome, and an even more intriguing method! I hope you found this exploration of the integral enjoyable. If you have any thoughts on this problem or Feynman’s technique, please feel free to share your insights.

Chapter 2: Feynman's Technique in Action

This video titled "Feynman's technique is the greatest integration method of all time" delves into the brilliance of Feynman's approach to integration and its historical significance.

In this follow-up video, "Feynman's Technique of Integration," you'll gain deeper insights into how this method can be applied effectively in various mathematical scenarios.