Chapter 1: Introduction to Density Functional Theory

Density Functional Theory (DFT) provides a framework for analyzing electron distribution in complex systems that go beyond simple hydrogen atoms. To model electron behavior, Schrodinger’s equation serves as the foundation, employing a fluid-like perspective. However, simulating the interactions between electrons poses significant challenges.

This section will outline the systems we aim to model, starting with the establishment of a Hamiltonian for an electron gas. Kohn and Hohenberg's seminal work examines the dynamics of inhomogeneous electron gases. Their Hamiltonian is comprised of three distinct components. The first component addresses the kinetic aspect of the field, represented by the squared gradient of the field. This mirrors the approach taken to model the kinetic energy of fluids. The equation below involves integrating the gradient's amplitude across the entire spatial domain, where phi denotes the creation operator and its complex conjugate signifies the annihilation operator.

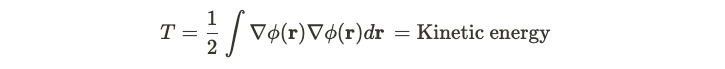
In quantum field theory, the creation operator is responsible for exciting the ground state, thus generating particles—this is akin to how creation operators function in a harmonic oscillator setup. The second component relates to the interaction of the field with an external potential, depicted by a lowercase v.

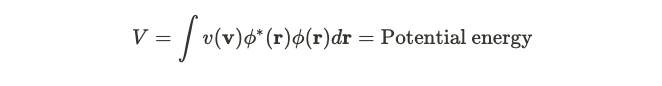
The third component encapsulates self-interaction within the gas, represented by the Coulomb term, which follows the form 1/r.

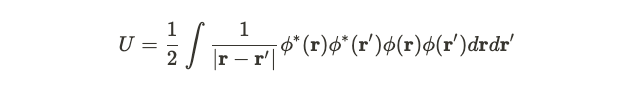
The total Hamiltonian is the aggregation of these three components.

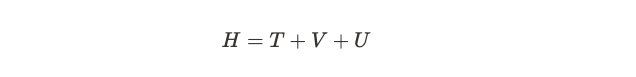
Similar to all quantum systems, this system possesses a ground state, which signifies the lowest energy configuration. From this ground state, we derive a crucial quantity known as electronic density. This density is calculated by contracting the ground state with both the creation and annihilation operators.

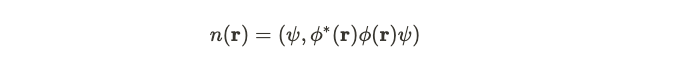
A pertinent question arises regarding the relationship between number density and the density v. Interestingly, the density indeed serves as a unique functional of the number operator. This insight allows us to establish the functional forms for both interaction and kinetic energy concerning the ground state.

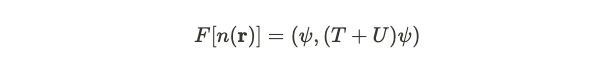
Chapter 2: Video Insights on Density Functional Theory

To deepen your understanding of Density Functional Theory, watch the following videos:

The first video titled "Introduction to Density Functional Theory [Part One] Background" provides foundational knowledge on DFT, explaining its significance and background.

The second video, "Density Functional Theory: Introduction and Applications," discusses the practical applications of DFT, emphasizing its relevance in various scientific fields.