Chapter 1: Introduction to Convex Hulls

One of the pivotal concepts in modern computational geometry is the Convex Hull. Its applications span various fields in engineering and science, prompting ongoing research aimed at optimizing related algorithms. While many challenges have been addressed, experts believe that there remains substantial potential for further exploration in both translational research and pure mathematics.

The applications of convex hulls include collision detection and avoidance, shape analysis, and finding the smallest enclosing box, among others.

To elucidate the concept of “WHAT IS A CONVEX HULL?”, let’s refer to Joseph O’Rourke’s analogy. He explains that the convex hull of a set of points in a two-dimensional space resembles the shape formed when a rubber band is stretched around nails driven into the plane at each point. In three dimensions, the boundary of the convex hull is akin to the shape created by tightly wrapping plastic around the points.

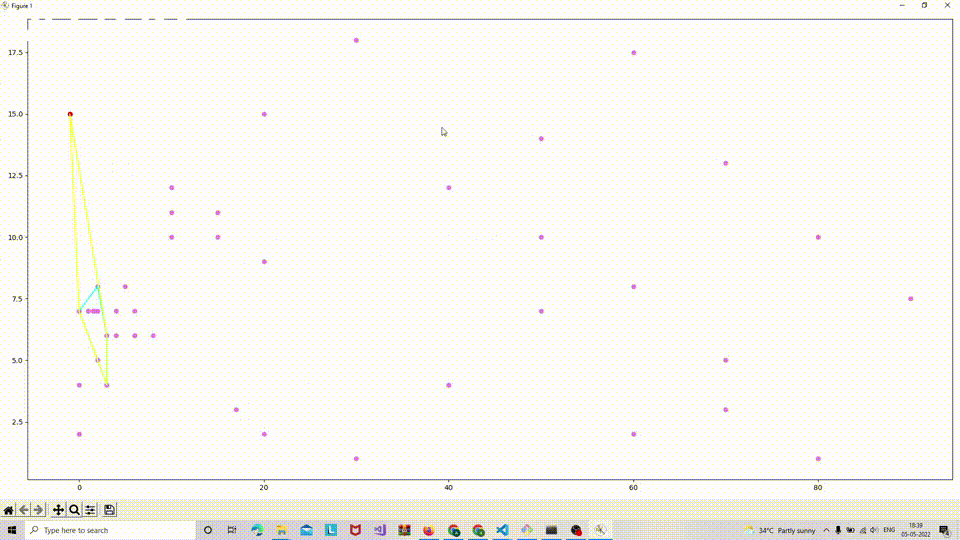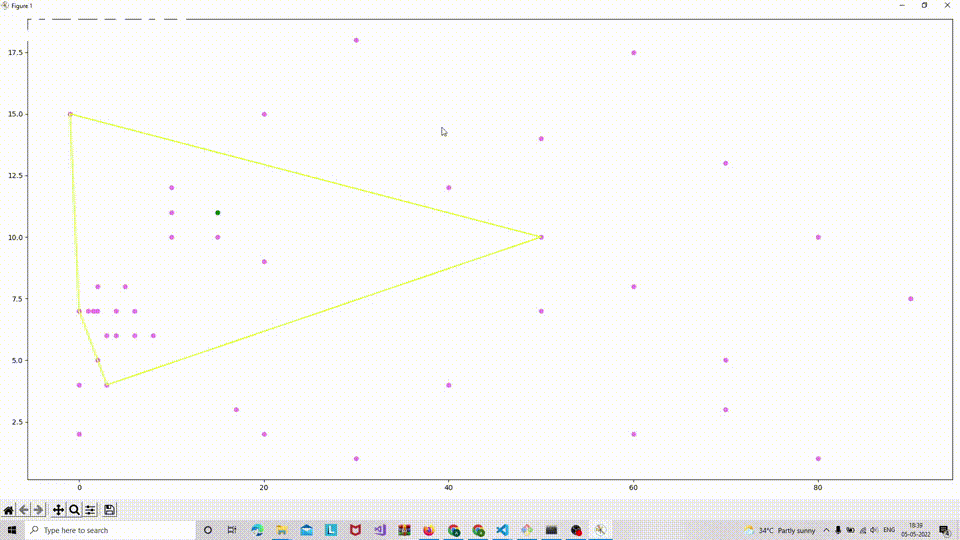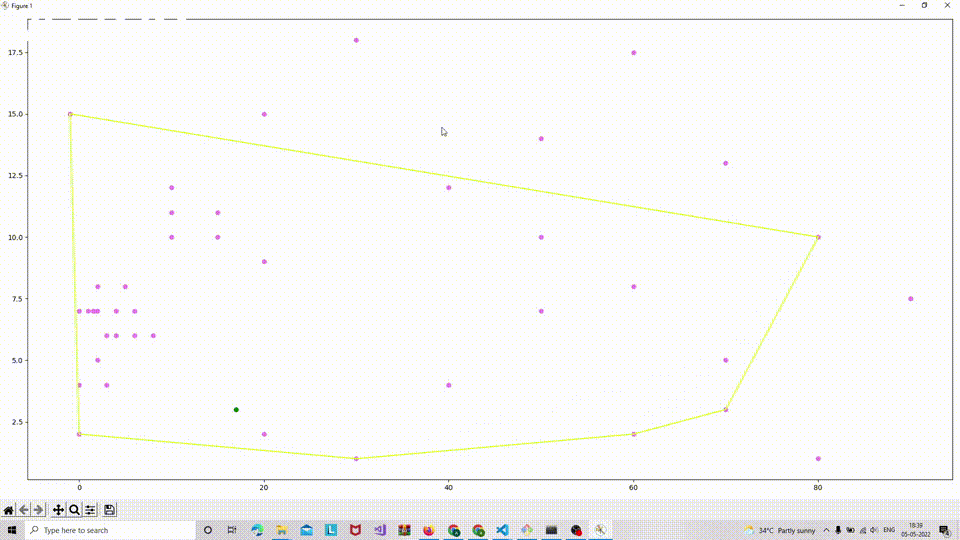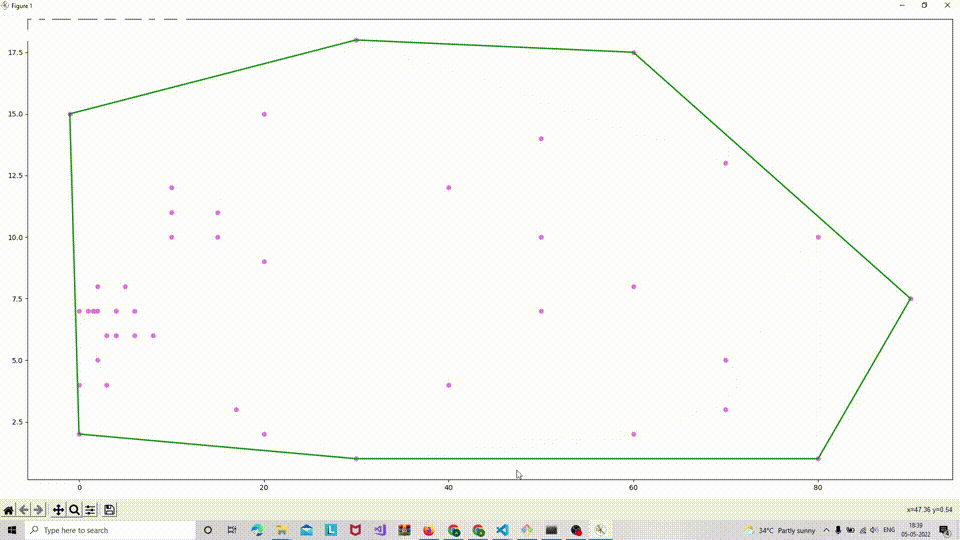
This is a visual representation of what a convex hull (depicted in green) looks like for a set of 350 points:

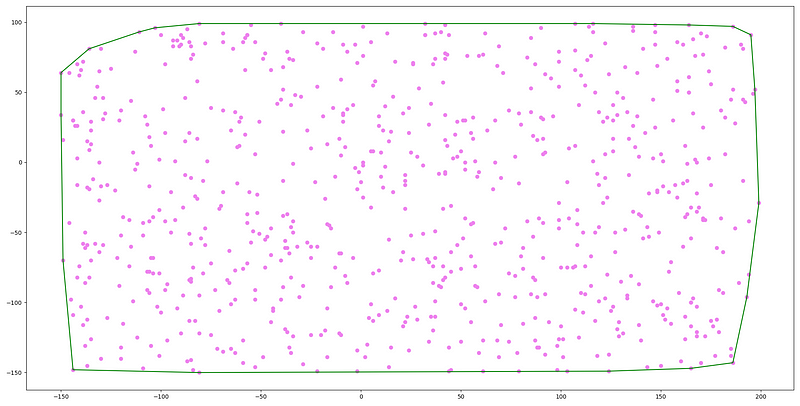
Chapter 2: The Importance of Convex Hulls in Robotics

To address the question of “Why are convex hulls utilized in robotic collision detection?”, consider a turtle bot navigating a 2D plane from point A to point B. The most straightforward route would be a direct line connecting these two points. However, should there be obstacles along this path, it becomes crucial to ascertain whether the robot collides with any of them in real-time or to confirm that the route is clear of obstructions as quickly as possible. This is where convex hulls come into play.

In this scenario, obstacles can be represented as points in a 2D space. By constructing a convex hull around these points, we can efficiently verify whether the robot's current position or any points along its intended path intersect with the hull. If any of these points lie within the hull, a collision is imminent; conversely, if all points remain outside the hull, the path is deemed free of obstacles. Thus, convex hulls significantly expedite the collision detection process.

Chapter 3: Computational Methods for Convex Hulls

Now, let’s explore “HOW ARE CONVEX HULLS COMPUTED?” Several algorithms can construct a convex hull for a given set of points. Below is a simplified overview of various algorithms, including their complexities and applicable scenarios:

1. Non-Extreme Points Identification: This method involves separating non-extreme points to identify extreme points, which ultimately yields the convex hull. Its complexity is O(n²) and it operates in 2D space.
2. Extreme Edges Identification: By isolating extreme edges within the point set, we can ascertain the convex hull. This method has a complexity of O(n³) and also functions in 2D space.
3. Gift Wrapping: A variation of the extreme edges identification, this algorithm begins with a single edge to facilitate the discovery of subsequent edges. Its complexity is O(n²) and is applicable in 2D space.
4. Quick Hull: This approach focuses on obvious points that are near the left and right extremes of the hull, which are initially identified through coordinate sorting. Its complexity is O(n log n) and works in 2D space.
5. Graham’s Scan: This technique incrementally constructs the hull around a sorted set of points. Its complexity is O(n log n) and is designed for 2D space.
6. Incremental Convex Hull: This method shifts the computational paradigm to enhance speed and enables calculations for 3D hulls. It has a complexity of O(n log n) and operates in both 2D and 3D spaces. Below is a gif illustrating the incremental algorithm in action.

7. Divide and Conquer: This approach divides the point set into equal halves, solving each recursively before merging results. Its complexity is O(n log n) and it is applicable in both 2D and 3D contexts.

To provide a practical understanding of implementing computational geometry algorithms, I have included a basic implementation of the incremental convex hull algorithm in Python. For a more comprehensive implementation, feel free to check out my repository.

The video titled "Differentiable Collision Detection for a Set of Convex Primitives" discusses advanced techniques for collision detection utilizing convex primitives, enhancing understanding of their practical applications in robotics.

The video "Understanding Physics: Collision Shapes, Mesh vs Hull, Concave vs Convex" provides insights into different collision shapes and their implications, crucial for effective collision detection strategies.

References:

• Computational Geometry in C — Joseph O’Rourke