Understanding the Law of Sines: A Comprehensive Guide
Written on
Chapter 1: Introduction to the Law of Sines
The Law of Sines states that the ratio of any side of a triangle to the sine of its opposite angle remains constant across all triangles.
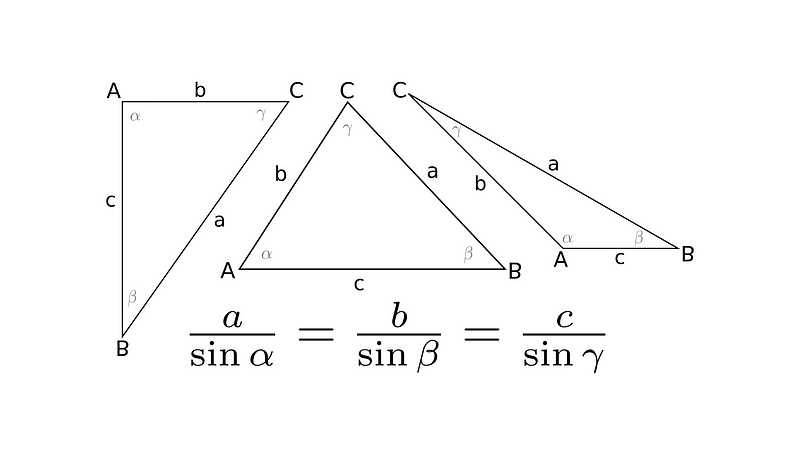
Triangles can be categorized based on their angles into three types: right, acute, and obtuse. The Law of Sines is applicable to all these types.
Section 1.1: Right Triangles
Consider a right triangle with vertices A, B, and C, where the angles are represented as ?, ?, and ? with ? being the right angle. The lengths of the sides opposite these angles are denoted as a, b, and c, respectively. This notation will be consistently used for clarity in upcoming examples.
To find the area of a triangle, multiply the length of any side by its corresponding altitude and then divide by two. It's important to note that two of the altitudes are the legs of the right triangle, while the third is not. Let's illustrate this.
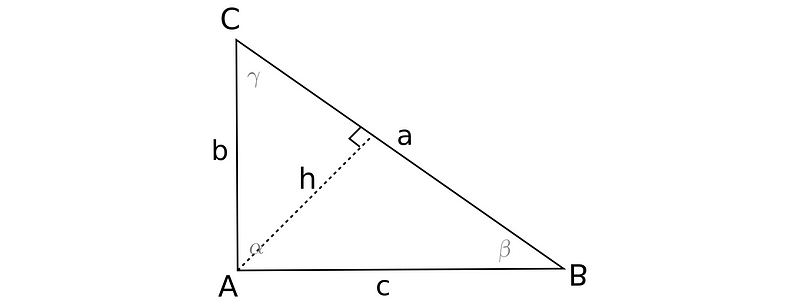
How do we determine the altitude h? Altitudes create right angles with the sides they intersect, allowing us to utilize right triangles to compute h through the sine function.
Let’s proceed with both triangles.
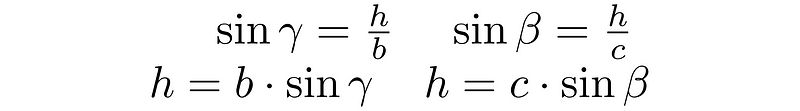
The area of triangle ABC can be calculated using both methods for h, plus an additional approach to incorporate all angle sines:
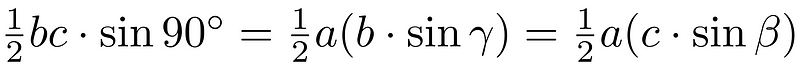
The goal is to demonstrate that the ratios of a side to the sine of its opposite angle are equivalent. For this to hold true, side lengths must correspond inversely with sin90°, sin?, and sin?.
To achieve this, each term in the above equation needs to be multiplied by 2/abc.
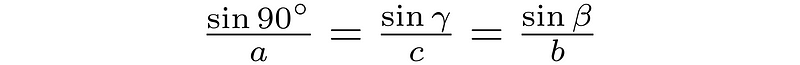
Taking the reciprocal of the equation yields the familiar form of the Law of Sines.
Section 1.2: Acute Triangles
Now, let's examine acute triangles. Here, all angles are less than 90°. The proof structure remains unchanged, but we need three distinct expressions for the area that incorporate the sine values of the angles.
To begin, we will again use two altitudes.
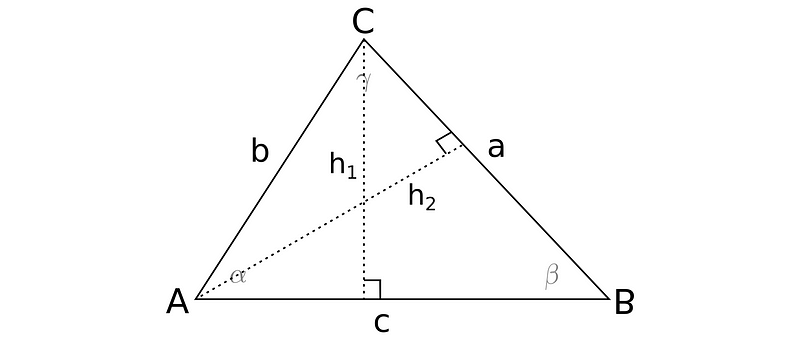
Next, we express the area using these altitudes.
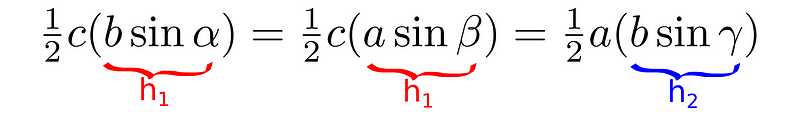
As before, we multiply by 2/abc.
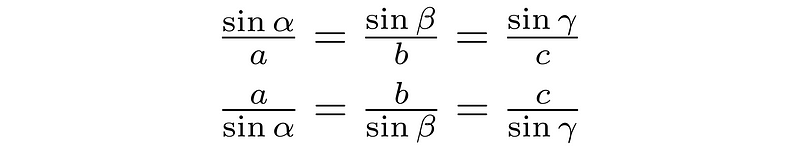
Section 1.3: Obtuse Triangles
The process for obtuse triangles follows a similar pattern, but with a crucial difference: only one altitude lies within the triangle while the other two are external. We need two altitudes for our calculations.
This is where the sine's supplementary angle identity becomes essential. The location of the altitude—inside or outside—does not affect the sine function, allowing us to proceed.
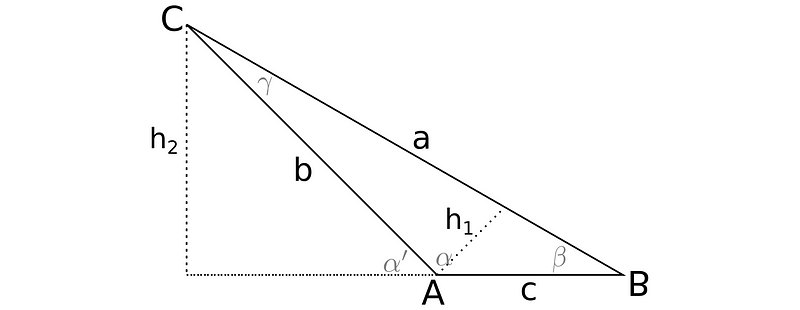
Now, we can write the area equations accordingly.
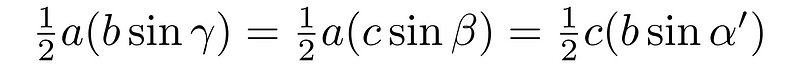
Since sin(θ') = sin(θ), we can express:
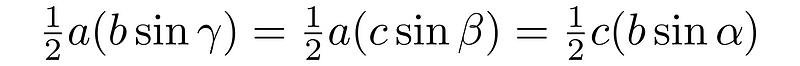
Finally, after multiplying by 2/abc and taking the reciprocal, we obtain the Law of Sines.
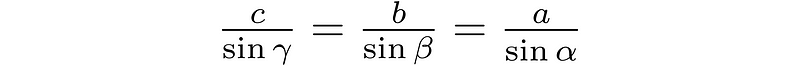
Until next time!
This video titled "PROOF of Law of Sines" provides a detailed explanation and demonstration of the Law of Sines, showcasing its applications in various triangles.
In the video "Law of Sines Visual Proof," viewers can visually grasp the concept of the Law of Sines through engaging demonstrations and examples.