Chapter 1: Introduction to Noether's Theorem

Noether's theorem reveals the fascinating relationship between symmetry and conserved quantities in physics. In my earlier discussion, I highlighted the intriguing outcomes derived from Noether's theorem, which posits that the presence of a continuous symmetry—such as rotational or translational—gives rise to a corresponding conserved current. This current is akin to a field characterized by direction and magnitude at each point in space, similar to the way electric currents flow through wires. Typically represented by the symbol J, Noether currents can be constructed from identified symmetries according to the guidelines provided by Noether's theorem.

Chapter 2: The Principle of Conservation

The fundamental aspect of Noether currents is that they adhere to a conservation principle. In this context, conservation signifies that the field is neither produced nor annihilated in a broad sense. To clarify this concept, let’s delve deeper into what this conservation principle entails. Essentially, it imposes limitations on the alterations a field can undergo in space. Intuitively, this law implies that a current cannot possess 'source' or 'sink' characteristics in spacetime. A 'source' refers to the phenomenon where a field appears to emanate from an empty region of space, similar to the idea that fields cannot spontaneously arise from nothing.

To simplify our understanding, we can temporarily set aside the complexities of spacetime and focus on a conserved field within pure spatial dimensions. An apt analogy would be the flow of water. We can refine our definition of a 'source' further. In physics, a field is often visualized as a series of arrows distributed throughout space. If at any particular point the number of arrows exiting exceeds those entering, we describe that point as a source, indicating a greater outflow of flux.

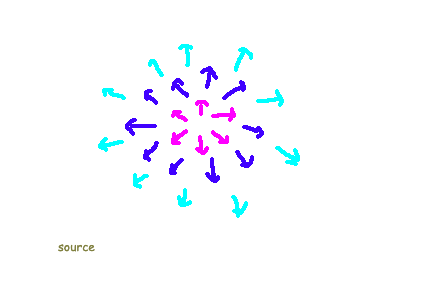
Similar reasoning applies to the concept of a 'sink.' A sink occurs when a field seems to dissipate into empty space. Using our earlier analogy, this means that at any given point in the field, the arrows pointing towards it cannot outnumber those pointing away from it. This suggests that the field cannot simply 'disappear' at certain locations and vanish into the void.

So, how does a conserved current field manifest? A conserved current in space must be devoid of any sinks or sources. A prime example of this is a field of vectors that all point in the same direction, as illustrated below.

Chapter 3: Noether Currents in Spacetime

In the framework of special relativity, it is crucial to treat time and space on an equal basis. This shift necessitates a slight adjustment to our conservation principle. Since the Noether current is a vector, it comprises four components that we must consider. The first component corresponds to the current moving in the time dimension, traditionally referred to as charge density. The remaining three components pertain to the spatial elements of the current. The full representation of the Noether current is typically denoted as follows, where the Greek letter rho represents charge density, and boldface J signifies the spatial components.

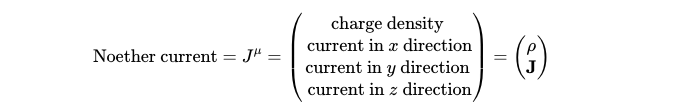
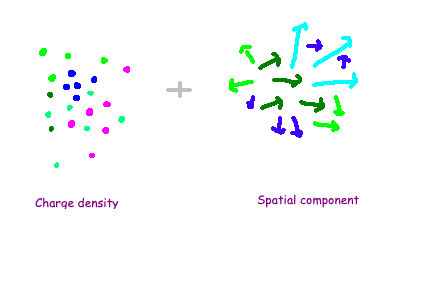
The charge density itself is quantified at every spatial point. In the subsequent diagram, various colors depict differing charge density values. Conversely, the spatial aspect of the current is represented by arrows assigned to each spatial point. The Noether current thus emerges as a combination of these two mathematical constructs, with the first field represented in the initial component and the spatial part encapsulated in the last three.

Mathematically, the absence of 'sources' or 'sinks' in spacetime can be articulated through the following equation. The first term illustrates the temporal evolution of charge density, while the second term addresses the 'sourceness' or 'sinkness' of the spatial Noether current. The conservation principle asserts that the rate of change of charge density over time, along with the divergence of J, should equal zero. Here, divergence is a mathematical operation that represents the concept of 'source' or 'sink' in spatial dimensions, denoted by the upside-down triangle in the equation below.

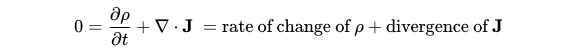
The equation above encapsulates the comprehensive conservation law for Noether's current. In the upcoming discussion, I will explore how physicists can derive a 'charge' from the Noether current, which can ultimately lead to the generation of massless particles.