Reference Frames

Special relativity fundamentally addresses how identical physical phenomena are perceived by observers in differing reference frames. Notable principles associated with special relativity—such as mass-energy equivalence, the impossibility of time travel, the light speed limit, and redshift—stem from these foundational assumptions.

To mathematically articulate the laws governing a physical system and measure its properties, a coordinate system is essential. However, these systems are purely mathematical constructs, and Nature does not inherently require the existence of any specific coordinate system. To employ one, we must first establish a reference, which includes a location in physical space and a set of perpendicular axes intersecting at that point. This allows us to define a Cartesian coordinate system, where these axes serve as the reference lines and their intersection acts as the origin. Together, the coordinate system and the reference form what we call a reference frame.

The position of the origin and the orientation of the axes will always relate to a physical object or set of objects. For instance, consider an observer on a train, with the x-axis directed towards the train's front, or at the center of a cube with axes perpendicular to its faces. We can define multiple reference frames for the same physical scenario; for example, one could describe a frame linked to a person observing a train from the platform, while another could be tied to an observer watching a rotating cube. Here, the reference frames are in relative motion.

It's crucial not to conflate the coordinate system with the reference frame. A coordinate system is a function mapping spatial points to ordered tuples of numbers, and it is nonsensical to claim that an abstract mathematical function is moving through physical space. For our purposes, this function is defined by the reference. For example, in a two-dimensional Cartesian coordinate system, a point P is represented as F(P) = (x(P), y(P)), where x(P) is the perpendicular distance from P to the y-axis and y(P) is the perpendicular distance from P to the x-axis:

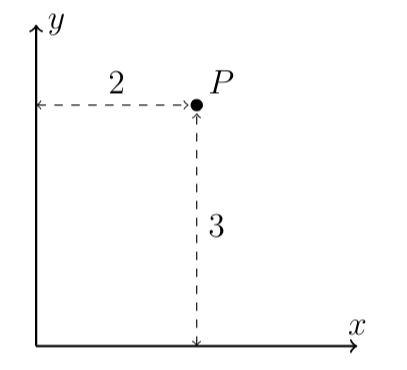
In this scenario, F(P) = (2, 3) indicates that the coordinates of point P are (2, 3).

We will primarily focus on inertial reference frames—those moving at a constant velocity relative to each other without acceleration or rotation. While special relativity can address non-inertial frames, provided gravity isn't the cause of acceleration (which requires general relativity), we will postpone that discussion for later in this series. The rationale behind this limitation is that if absolute velocity could be detected, it would enable the definition of an absolute reference frame, contradicting the notion that Nature lacks an inherent coordinate system. However, absolute accelerations can be detected since they imply forces, and a force either acts or does not. If this were not true, a physical process could manifest in one frame but not in another, violating our first postulate.

Typically, we observe scenarios where an experimenter monitors the motion of an object, ensuring that neither the observer nor the object experiences acceleration. The unique frame where the object remains stationary is known as the rest frame (or proper frame) S', while the frame where the observer is at rest is called the observer frame (or lab frame) S. Generally, distinguishing between the two should be straightforward. Additionally, we assume both frames are in standard configuration, meaning S' moves at a constant velocity along the x-direction relative to S, their coordinate origins coincide at t = t' = 0, and their axes remain parallel:

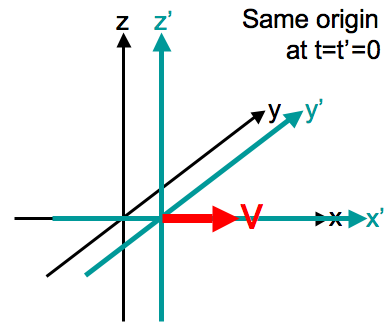
The coordinates in the rest frame are denoted with primes (t', x', y', z'), while the observer frame coordinates are simply (t, x, y, z), linked by the Lorentz transformation:

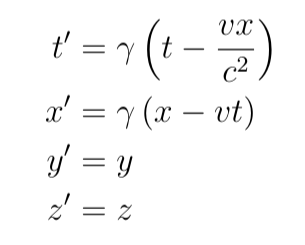
We will typically overlook the y and z coordinates.

The symbol γ represents the Lorentz factor:

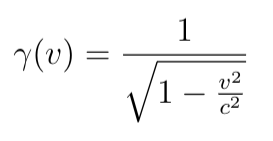
One final note before progressing: if an object has a length L in frame S and L' in frame S', or if the time interval between two events is Δt in frame S and Δt' in frame S', or if a particle's speed is U in frame S and U' in frame S', I will not assert that L, Δt, and U "appear" to have different values in varying frames. The term "appear" suggests that the discrepancies between values across frames signify an error or illusion that detracts from a single "true" value, which is not accurate. There is no absolute "true" length of an object, no universally valid time interval between events, and no definitive speed for a particle, as measuring these quantities necessitates a coordinate system, thus requiring a reference frame. Since no single "correct" reference frame exists, there is no singular "correct" value for these measurements.

Now, let’s delve into the core of our discussion and utilize the insights from special relativity regarding reference frames to examine some physical challenges.

Section 1.1: Invariance of Causality and the Speed Limit

Observing a physical system from a different reference frame does not alter the underlying physics governing that system. Consequently, if something holds true in one frame, it must also be valid in all others, although the rationale behind its truth may vary. In simpler terms, changing one's frame of reference does not alter the fundamental truths of Nature, one of which is the causal relationships between physical events. If event A causes event B in one frame, then there is no frame in which B causes A; this principle is known as the invariance of causality.

We can employ the invariance of causality to comprehend what is meant by c as the "universal speed limit." Suppose frame S exists where event A causes event B through the transmission of a faster-than-light signal, such as firing a bullet at speed U > c. In this frame, let Δx represent the distance between the two events and Δt denote their time separation, such that U = Δx/Δt. Since event A precedes event B in frame S, Δt must be positive. Now, let S' be a frame moving with speed v < c relative to S. By the Lorentz transformation:

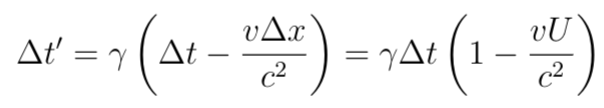
If c²/U < v < c, which is permissible since all speeds under c are allowed, we have identified a reference frame where Δt' is negative, indicating that in this frame, B occurs before A, which is impermissible.

This implies that if one event leads to another, it must do so through a signal traveling at or below the speed of light. This notion is often expressed as "Information cannot exceed the speed of light." Yet, we will see later that a signal may traverse from event A to event B at a speed greater than c without allowing event A to cause event B.

Section 1.2: The Relativity of Simultaneity: The Case of the Fast Snake

Imagine a swift snake escaping from its enclosure in the biology lab, racing across a table at 0.6c. Its proper length (the length measured in its rest frame) is precisely one meter. A student intends to ensnare the snake using a one-meter-wide rectangular net by dropping it at the perfect moment, ensuring the net lands just behind the snake's tail while the front edge lands ahead of its head. If the net strikes the snake, the animal will be harmed, and the student will face reprimand from her advisor.

The student argues: "In my rest frame, the snake moves at 0.6c, so its length contracts to 80 centimeters. This means the net's left rim will land just behind the snake's tail, while the right rim will rest 20 centimeters in front of its head, allowing me to catch it without injury."

The snake counters: "I am 100 centimeters long, and the net approaches me at 0.6c, causing its width to contract to 80 centimeters. If the left rim strikes the table just behind my tail, the right rim will hit me, resulting in injury, and you will be in big trouble!"

Ultimately, either the snake or the student must be incorrect. How can we resolve this paradox?

Let S represent the student's rest frame and S' the snake's rest frame. In S, let x = 0 be where the net's left edge hits the table at time t = 0, coinciding with when the snake's tail passes this point. In S', the frame where the snake is stationary, let x' = 0 mark the position of the snake's tail. Let t and t' indicate the times when the net's edges land in S and S', respectively.

At this moment, t' = t = 0s, x' = 0cm, and x' = 100cm. For v = 0.6c, γ = 1.25. Applying the Lorentz transformation:

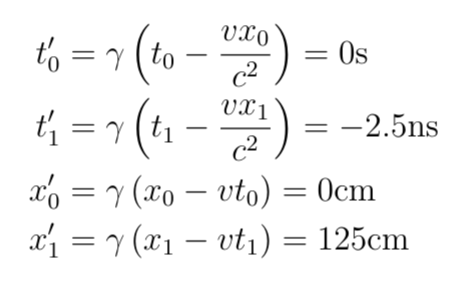
This reveals that the snake is mistaken. In its rest frame, the right edge of the net strikes the table 2.5 nanoseconds before the left edge. While it's true that the edges of the net are only 80 centimeters apart in the snake's frame, the timing discrepancy means they hit the table at distances of 125 centimeters apart.

Here’s how the snake perceives the event: The two edges are 80cm apart and approach it at 0.6c. The right edge contacts the table at t' = -2.5ns, 125cm ahead of the snake's tail (or 25cm in front of its head). At this time, the left edge is still hovering above the snake, 45cm in front of its tail. When t' = 0s arrives, 2.5 nanoseconds later, the left edge has traveled 0.6c * 2.5ns = 45cm towards the snake's tail, landing just behind it. Neither edge of the net strikes the snake.

The snake's error lies in overlooking the relativity of simultaneity: two events, A and B, occurring simultaneously in one reference frame do not necessarily happen simultaneously in another. Additionally, there are frames where A precedes B and vice versa. This does not violate the invariance of causality, as neither event causes the other. If A and B occur at the same time but in different locations, and if A were to influence B, it would necessitate an infinite-speed signal from A to B, which is impossible.

You might notice a potential issue: the right edge of the net continues moving towards the snake at 0.6c after hitting the table. Since it lands only 25cm in front of the snake, if the snake stops as its head meets the right edge, the left edge will still hit the snake 20cm in front of its tail. Does this jeopardize our argument?

Not at all. Assume the snake's head halts when it reaches the right edge, occurring at approximately t' = -1.39ns. Even if we assume the snake is entirely rigid, its tail will not stop simultaneously, as the head's stopping is causally linked to the tail's stopping. Thus, the tail cannot halt before a signal (a nerve impulse or shock wave) traveling no faster than light reaches it. The snake's total length is one meter, and the time required for a signal to traverse one meter at light speed is about 3.33 nanoseconds. Consequently, the tail continues moving long enough to evade being struck by the left edge of the net.

The Faster-Than-Light Laser Dot Paradox

Now consider another classic scenario. Imagine an astronomer on Earth shining a powerful laser at the Moon, strong enough to create a visible dot on its surface. The astronomer sweeps the laser across the Moon's equator—approximately 3,393 miles—within 0.01 seconds. An observer on the Moon witnesses the dot racing by at about 1.82c. Doesn’t special relativity assert that nothing can travel faster than light? Have we uncovered a flaw in the theory?

The answer is no, as special relativity does not claim that “nothing” can exceed the speed of light. What it clarifies is that one event cannot influence another if doing so necessitates that the first event send a signal to the location of the second event at a speed surpassing c. In this scenario, the laser dot can move from point A to point B faster than light because the appearance of the dot at point A does not cause its subsequent appearance at point B. In a later discussion on special relativity concerning rotating frames, we will demonstrate that there exists a reference frame where the dot reaches B before arriving at A.

Twisting of a Spinning Rod

To illustrate a final example, consider a straight cylindrical rod in frame S' rotating with angular speed ω. In frame S, the rod not only rotates but also advances with a velocity of +vx. We will discover that the rod appears twisted along its length in frame S.

Starting from frame S', divide the rod into disks spaced by one unit distance Δx' = 1. Treat these disks as clocks, each marked with a single hand oriented identically. This is how the disks appear in S':

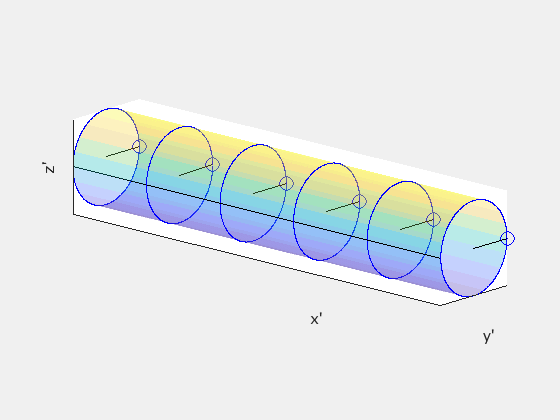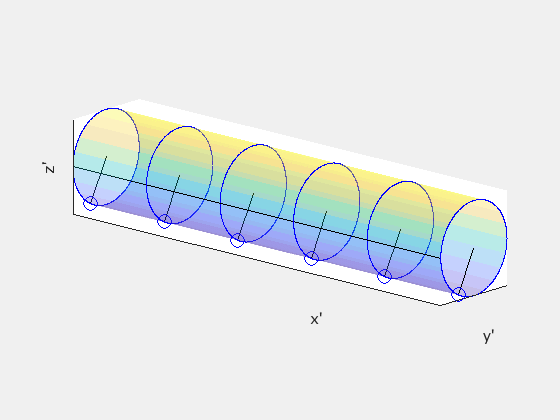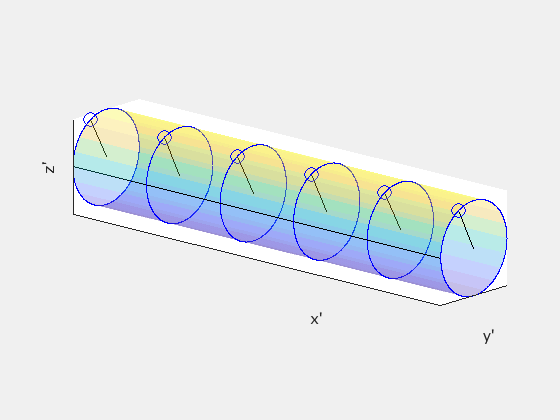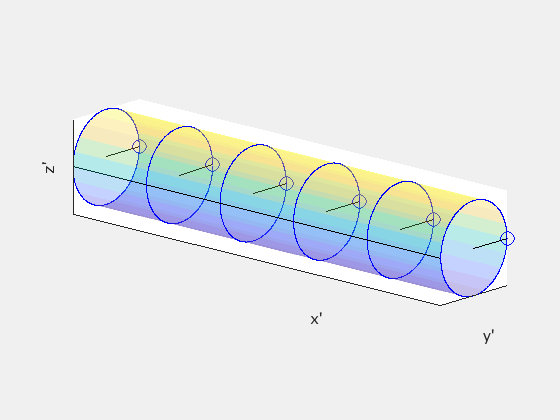
In S', neighboring hands strike the black line simultaneously. However, due to the relativity of simultaneity, this is not the case in any other frame. Given Δx' = 1 and Δt' = 0, let’s determine Δt in the observer frame S using the inverse Lorentz transformation:

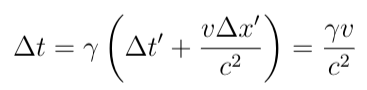
This indicates a time delay of Δv/c² between neighboring hands passing the black line. Since ω denotes the angular frequency for a complete rotation, neighboring hands will be offset by a phase angle of ωΔv/c². Note that ω maintains the same value across both frames as the angular motion occurs perpendicular to the rod's velocity. Ignoring the rod's forward motion, this is how the clocks would appear in frame S:

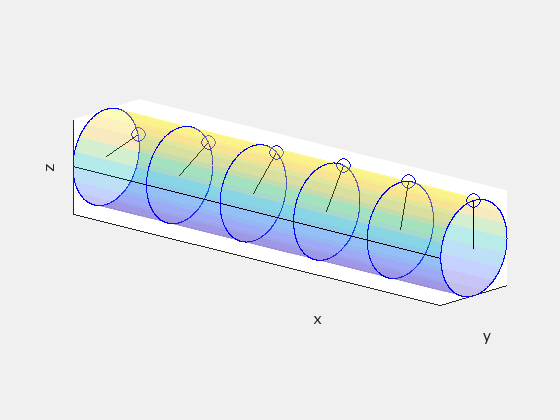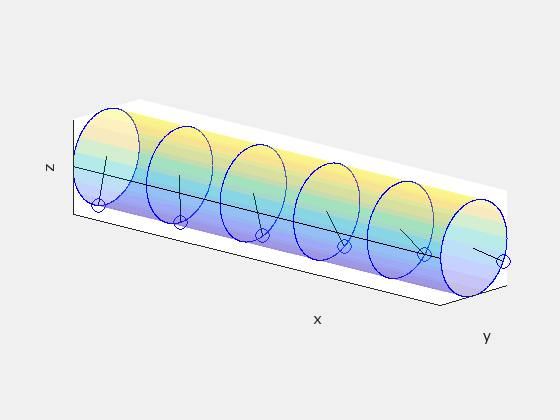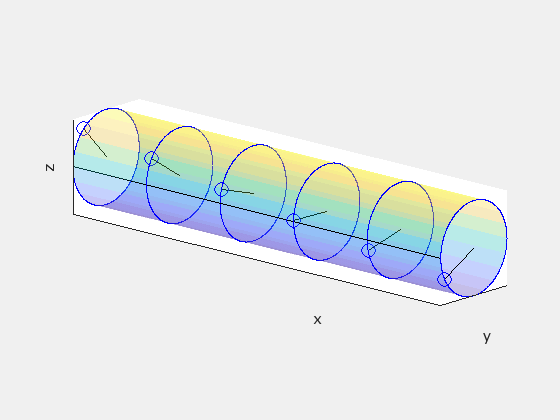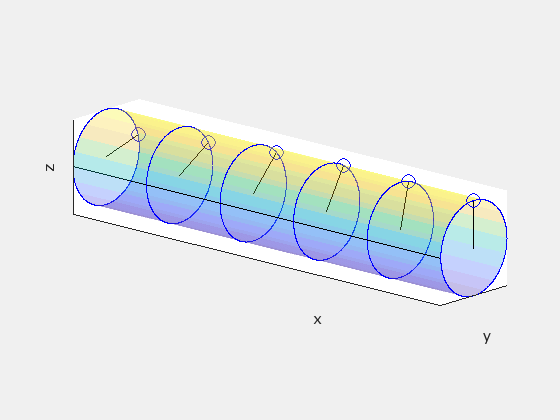
This demonstrates that the rod must exhibit twisting about its axis in frame S. The following animation compares the rod's appearance in both frames, with S' on the left and S on the right:

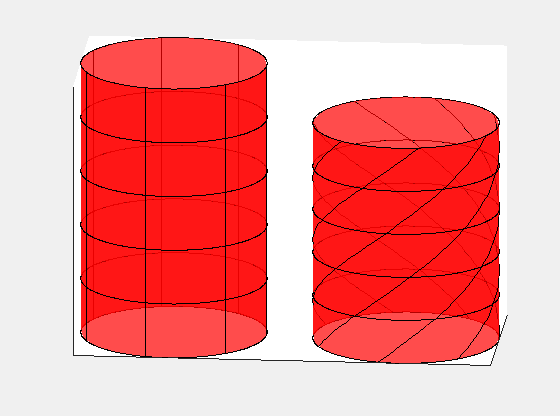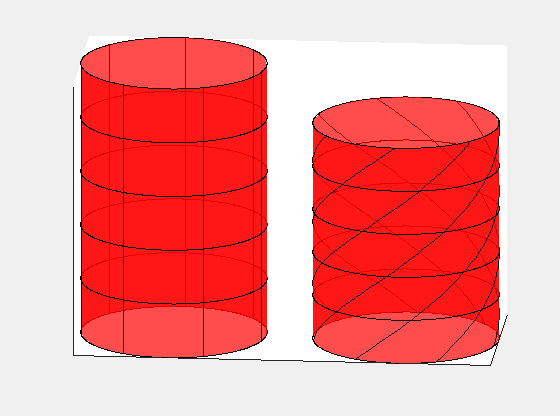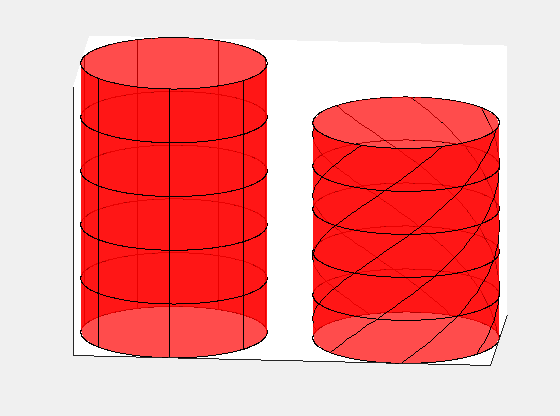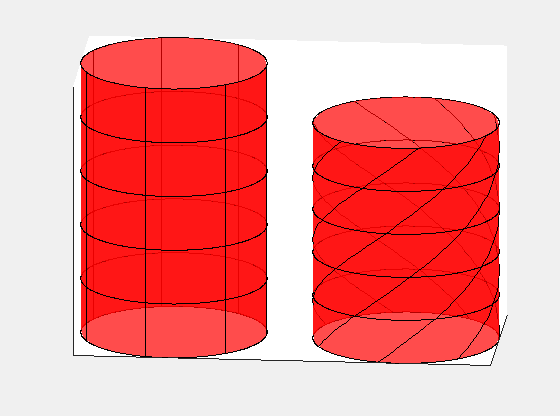
Note: The intensity of the twisting is exaggerated for clarity.

The rod is not undergoing any twisting force or mechanical deformation; rather, the geometry of the rod differs between the two reference frames.