How Fast Must Wonder Woman's Lasso Spin to Deflect Bullets?
Written on
Chapter 1: Understanding the Physics of Wonder Woman's Lasso
It's clear that Wonder Woman is a fictional character, and I’m perfectly fine with that. The fact that she performs feats that defy conventional physics only adds to the allure of superhero films like Wonder Woman 1984. However, this doesn’t mean I can’t enjoy the movie while also delving into the underlying physics. Let’s take a closer look.
In one notable scene from the trailer, Wonder Woman is depicted spinning her lasso to intercept a barrage of bullets. Here’s the full trailer for reference, but the part I'm focusing on is the bullet-blocking action.

Now, the pressing question arises: How quickly must she rotate her lasso to effectively block bullets? Let’s analyze this scenario.
Section 1.1: Directly Blocking Bullets
To start, let’s imagine the lasso as a cylindrical object with length ( L ) and diameter ( d ), rotating with an angular velocity ( omega ). Here’s a rough illustration to visualize this setup.
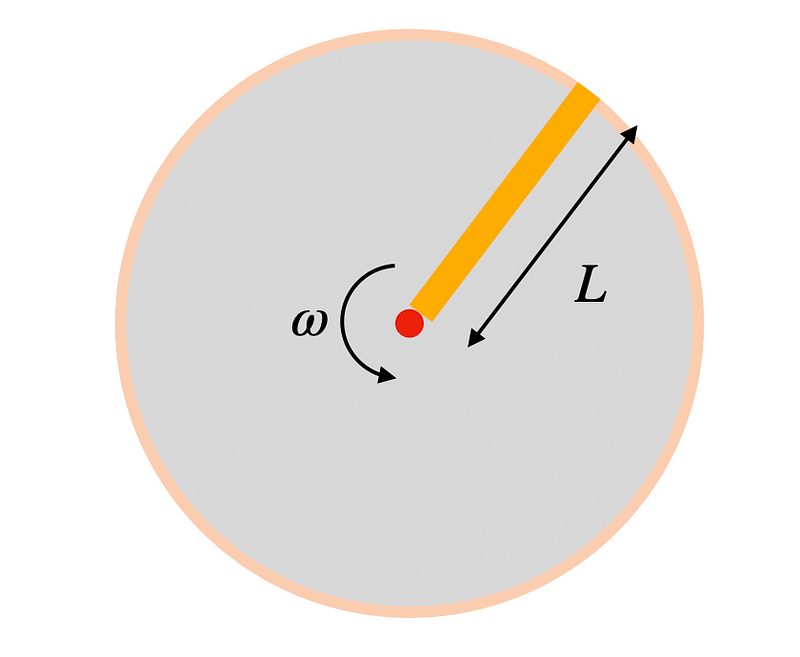
Assuming Wonder Woman spins the lasso at a constant angular speed—meaning she’s not precisely targeting the bullets but instead whirling the lasso fast enough to catch them in its path—the probability of a bullet striking the lasso can be calculated. This probability depends on the ratio of the lasso’s cross-sectional area to the area swept by its circular motion, independent of the lasso’s rotation speed.
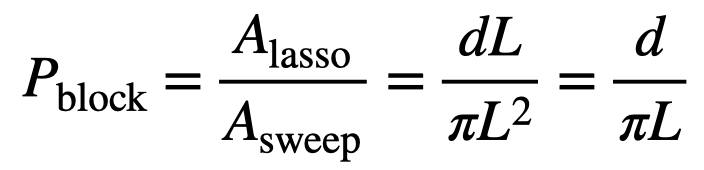
Given this setup, it’s clear that the lasso’s efficiency at blocking bullets is questionable. However, we can explore another method.
Section 1.2: Deflecting Bullets
This brings us to a potentially more effective approach: what if the lasso impacts the side of a bullet as it travels through the area swept by the spinning lasso? This magical lasso could alter the bullet's trajectory and redirect it away from its target.
Let’s represent the bullet as a cylinder, traveling at a velocity ( v ).
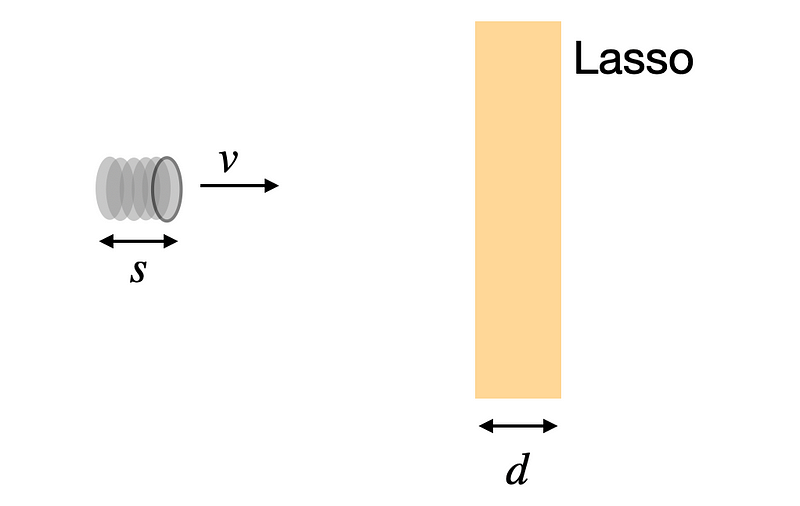
For the bullet to clear the lasso’s path, it needs to travel a total distance of ( s + d ), where ( s ) is the length of the bullet. If the bullet moves with a constant speed ( v ), the time taken to pass through the lasso's sweeping area can be expressed as:
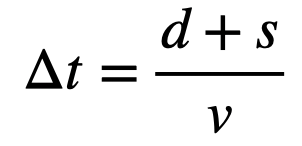
Now, if the bullet enters the area right after the lasso has swept by, the lasso must complete almost a full revolution during the bullet’s travel time. Therefore, we can calculate the required angular velocity ( omega ) of the lasso. The change in angle will be approximately ( 2pi ) radians.
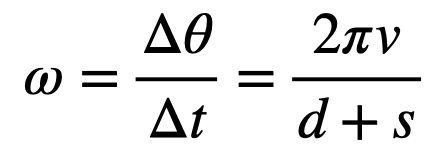
To carry out these calculations, I’ll use some estimated values:
- Bullet speed: between 400 m/s (9 mm) and 960 m/s (M855A1 round from an M16)
- Bullet length: approximately 1.3 cm to 2.1 cm
- Lasso diameter: around 1 cm (estimated)
- Lasso length: roughly 1.5 meters
With these values, I’ll apply a simple Python script for calculations, allowing for adjustments to the input parameters.

The calculations reveal staggering results: approximately one million revolutions per minute for lower-end bullet speeds. This leads to another calculation of the lasso's tip speed as it sweeps through the area.
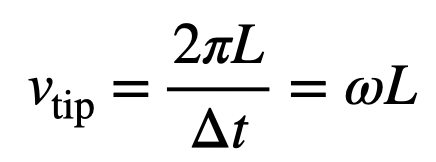
With the same parameters, the tip speed reaches ( 1.8 times 10^6 ) m/s, which is significantly faster than the speed of sound (343 m/s), resulting in a Mach speed of around 528. This would undoubtedly produce an impressive sonic boom.
Chapter 2: The Reality of Spinning the Lasso
The first video titled The Secret of Wonder Woman's Bullet Blocking! (Because Science w/ Kyle Hill) delves into the science behind Wonder Woman's iconic ability to deflect bullets with her lasso.
In another video, WONDER WOMAN Lasso's the MAJOR‼️ Bullets and Bracelets & Golden Lasso, we see further exploration of Wonder Woman's lasso techniques and their effectiveness.