The Question

We have two functions, f(x) and g(x), defined below, which possess the same minimum value.

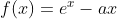
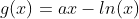
The task is to:

1. Demonstrate that there is a straight line y = b which intersects both f(x) and g(x) at three points in total, with the x-coordinates of these intersection points forming an arithmetic progression.

The Solution

Part 1

When a ≠ 0, the derivative f’(x) is positive, indicating that f(x) is monotonically increasing, which implies a must be greater than 0.

When a > 0, f’(x) is negative on the interval (-∞, ln(a)) and positive on (ln(a), ∞), indicating that f(x) decreases until ln(a) and then increases, confirming the existence of a minimum value at f(ln(a)) = a - a ln(a). Similarly, for g(x), we find a minimum at g(1/a) = 1 + ln(a).

Since both functions share the same minimum value, we derive the equation:

a - a ln(a) = 1 + ln(a)

A straightforward solution for a is 1, which indeed satisfies the equation since it is monotonically increasing for a > 0, confirming that a can only equal 1. Readers are encouraged to explore this further by calculating the gradient of the equation.

Part 2

1. Intersection Points

From Part 1, we established that both f(x) and g(x) reach a minimum of 1, which necessitates that b in the line y = b be greater than 1 for it to intersect f(x) and g(x) at least twice.

For y = b to intersect f(x) twice, we need F(x) = f(x) - b = 0 to have two solutions. Since

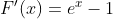
F(x) is decreasing on (-∞, 0) and increasing on (0, ∞), we need to verify that F(0) < 0. This holds true since F(0) = 1 - b < 0 for b > 1, thus y = b intersects f(x) at two points.

Let’s denote these intersection points as x₁ and x₂, where -∞ < x₁ < 0 and 0 < x₂ < ∞.

For y = b to intersect g(x) twice, we require G(x) = g(x) - b = 0 to have two solutions. Since

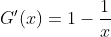
G(x) is decreasing on (0, 1) and increasing on (1, ∞), we check that G(0) < 0, which is valid as G(0) = 1 - b (with b > 1). Therefore, y = b intersects g(x) at two points, denoted as x₃ and x₄, with 0 < x₃ < 1 and 1 < x₄ < ∞.

2. Arithmetic Sequence

Next, we need to prove that there exists a value of b such that x₁ = x₃. If this condition is met, then y = b will intersect both f(x) and g(x) at three points.

Let F(x₃) = G(x₃) = 0. Thus, we derive

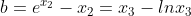
Substituting x₁ with x₃ leads to (Equation 1), which has a solution in the interval (0, 1). This can be demonstrated by identifying x₁ values in (0, 1) yielding both negative and positive outputs for the equation.

Now we conclude that x₁ corresponds to x₃, provided Equation 1 is satisfied.

Finally, we must show that x₄ - x₁ = x₂ - x₃, establishing that x₁, x₂, and x₃ indeed form an arithmetic sequence.

As

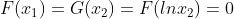
It follows that, with x₁ < 0 and x₂ in (0, 1) leading to ln(x₂) < 0, and knowing F(x) is decreasing in the interval, we find that x₂ = ln(x₁), ensuring a one-to-one correspondence for x and F(x).

Similarly, with x₄ > 1 and x₃ in (0, 1), we deduce e^x₄ > 1, and since G(x) is increasing in (1, ∞), we confirm that x₄ = e^x₃.

By substituting these into the equation x₄ - x₁ = x₂ - x₃, we verify that it satisfies Equation 1, thereby completing the proof.

How did you approach solving this complex problem?