Proving the Parallelogram Property in Quadrilaterals
Written on
Chapter 1: Understanding the Problem
In this exercise, we examine a convex quadrilateral ABCD. The midpoints of its sides, denoted as E, F, G, and H (for AB, BC, CD, and DA respectively), play a crucial role in our proof. We are tasked with proving that if the lines AC, BD, EG, and FH all intersect at a single point O, then ABCD must be a parallelogram.
To facilitate this, we will reference a useful tool: The Theorem Grid, which outlines the relevant theorems we will utilize throughout our proof.
Introducing: The Theorem Grid
A collection of theorems related to Euclidean geometry.
Section 1.1: The Path to Proving ABCD is a Parallelogram
According to Theorem 1.9, we only need to demonstrate that the diagonals AC and BD bisect each other to establish that ABCD is a parallelogram. To achieve this, we will identify midpoints on both diagonals and prove their coincidence.
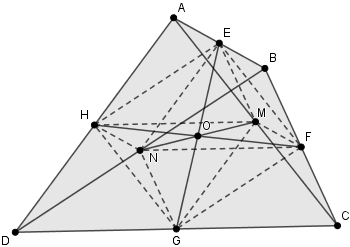
Let M and N represent the midpoints of AC and BD, respectively. By applying Theorem 1.1, we find that triangles DHG and DAC are congruent, as are triangles BEF and BAC. Consequently, we establish that segments HG and EF are equal to half the length of AC, confirming that EFGH is indeed a parallelogram. Given that EG and FH are the diagonals of EFGH, their intersection at point O indicates that they bisect each other at that point, meaning O is the midpoint of FH.
Furthermore, leveraging Theorem 1.1 once more, we see that triangles HAM and DAC are congruent, and triangles NBF and DBC are also congruent. This results in segments HM and NF being equal to half the length of DC, which shows that HMFN is also a parallelogram. As before, since NM and FH intersect at O, Theorem 1.9 guarantees that MN must also pass through O, indicating that O is the midpoint of MN.
At this stage, we have established that EG, FH, and MN all intersect at O and bisect one another.
Section 1.2: Concluding the Proof
Since M is defined as lying on segment AC (being its midpoint), and given that O is the intersection of AC and BD, it must also lie on AC. The collinearity of points M, O, and N signifies that if M and O are on AC, N must also reside there. Since N is already established as lying on AC and is also defined as the midpoint of BD, it becomes evident that N coincides with O.
Utilizing similar reasoning, we can also conclude that M coincides with O.
Thus, both O and M are identified as the midpoints of diagonals AC and BD, respectively. By invoking Theorem 1.9, we conclude that ABCD must indeed be a parallelogram.
Endnote
You may notice that the accompanying figures do not explicitly show the coincidences of M, N, and O. This choice was intentional to maintain a general representation and mitigate bias in our approach, as we aim to prove that ABCD can be a parallelogram.
Additionally, observant readers may find that the quadrilateral ABDC bears resemblance to the Geoclid logo. If you recognized this, well done!
Chapter 2: Further Exploration
This video showcases the Indian Mathematical Olympiad (RMO 2011 Question 6), providing insights into the problem-solving techniques relevant to the topic.
In this segment, Shibendra Singh discusses CRMO 2011 Problem 4, focusing on combinatorial strategies within the Cheenta Math Olympiad Program.